ajout des fichiers
54
0_cours.tex
Normal file
|
|
@ -0,0 +1,54 @@
|
|||
%\documentclass[11pt,a4paper,DIV=calc]{scrartcl}
|
||||
\documentclass[9pt,a4paper]{article}
|
||||
\usepackage[margin=2.5cm]{geometry}
|
||||
|
||||
\usepackage{pdfpages}
|
||||
\usepackage[french]{babel}
|
||||
\usepackage[utf8]{inputenc}
|
||||
\usepackage{libertine}
|
||||
\usepackage{amsmath}
|
||||
\usepackage{hyperref}
|
||||
\usepackage[T1]{fontenc}
|
||||
\usepackage{amssymb}
|
||||
\usepackage{mathrsfs}
|
||||
%\usepackage{frcursive}
|
||||
|
||||
\usepackage{graphicx}
|
||||
\usepackage{empheq}
|
||||
%\KOMAoptions{DIV=last}
|
||||
\newcommand{\D}{\Delta}
|
||||
\newcommand{\deriv}{\mathrm{d}}
|
||||
|
||||
\newcommand{\n}[3]{\prescript{#2}{#3}{\mathit{#1}}} % pour écrire les atomes
|
||||
\newcommand{\He}{\n{He}{4}{2}} % particule alpha
|
||||
\newcommand{\neu}{\n{\nu}{0}{0}} % neutrino
|
||||
\newcommand{\aneu}{\n{\overline{\nu}}{0}{0}} % antineutrino
|
||||
\newcommand{\A}{\mathscr{A}} % activité
|
||||
\newcommand{\ex}{\mathrm{e}}
|
||||
\newcommand{\ra}{\longrightarrow}
|
||||
\newcommand\vect[1]{\overrightarrow{#1}}
|
||||
|
||||
\author{
|
||||
Professeur : Étienne Gravier \\
|
||||
{\small \texttt{\href{mailto:Etienne.Gravier@univ-lorraine.fr}{Etienne.Gravier@univ-lorraine.fr}}}\\
|
||||
Auteur : Louis-Guillaume Dubois\\
|
||||
{\small \texttt{\href{mailto:Louis-Guillaume.Dubois@supelec.fr}{Louis-Guillaume.Dubois@supelec.fr}}}
|
||||
}
|
||||
\title{Physique nucléaire, relativité et plasmas\\
|
||||
Notes de cours}
|
||||
|
||||
|
||||
\begin{document}
|
||||
\maketitle
|
||||
|
||||
%\titlepage
|
||||
\tableofcontents
|
||||
%\pagebreak
|
||||
|
||||
\input{1_hist}
|
||||
\input{2_rr}
|
||||
\input{3_rr2}
|
||||
\input{4_noyau}
|
||||
\input{5_rp}
|
||||
|
||||
\end{document}
|
||||
178
1_hist.tex
Normal file
|
|
@ -0,0 +1,178 @@
|
|||
|
||||
|
||||
\part{Historique}
|
||||
\subsection*{Moyen-Âge : découverte de la pechblende}
|
||||
|
||||
|
||||
Un minerai particulier est signalé en Saxe : la \textbf{pechblende},
|
||||
mais pendant longtemps il n'a présenté que peu d'intérêt :
|
||||
on pensait qu'il ne contenait que du fer et du zinc.
|
||||
\marginpar{
|
||||
\includegraphics[width=20mm]{Pichblende.eps}\\pechblende
|
||||
%« Pichblende » par Original uploader was Kgrr at en.wikipedia — Originally from en.wikipedia; description page is/was here.. Sous licence Creative Commons Attribution-Share Alike 2.5 via Wikimedia Commons - https://commons.wikimedia.org/wiki/File:Pichblende.jpg#mediaviewer/File:Pichblende.jpg
|
||||
}
|
||||
En réalité ce minerai est constitué de dioxyde d'uranium $UO_{2}$.
|
||||
De nos jours on trouve l'uranium au Congo, au Canada, en Russie,
|
||||
au Khazakhstan, en Namibie et au Niger.
|
||||
|
||||
|
||||
\subsection*{1789 : découverte de l'Uranium par Klaproth}
|
||||
Un chimiste allemand, Martin Heinrich Klaproth (1743--1817),
|
||||
annonce en 1789 l'existence dans la penchblende d'un métal nouveau
|
||||
qu'il appelle \textbf{uranium}, en référence à la planète Uranus
|
||||
découverte 8 ans plus tôt.
|
||||
\marginpar{
|
||||
\includegraphics[width=20mm]{Klaproth.jpg}\\Klaproth
|
||||
%Par Mutandis (Travail personnel) [GFDL (http://www.gnu.org/copyleft/fdl.html) ou CC-BY-3.0 (http://creativecommons.org/licenses/by/3.0)], via Wikimedia Commons
|
||||
}
|
||||
|
||||
Cependant ce métal restera sans grand intérêt pendant encore un siècle.
|
||||
Il a longtemps été considéré inoffensif.
|
||||
|
||||
Cet élément possède une radioactivité très faible, difficilement détectable sans instrument précis.
|
||||
On compte dans l'uranium 99,3\% de $^{238}U$, dont la période de demi-vie s'étend sur 4,5 milliards d'années,
|
||||
et 0,7\% de $^{235}U$, dont la période est de 810 millions d'années.
|
||||
|
||||
\subsection*{1895 : découverte des rayons X par Röntgen}
|
||||
Le physicien allemand Röntgen (1845--1923) découvre un rayonnement, qu'il nomme rayons X car
|
||||
il ne sait pas de quoi il s'agit. En 1901 il recevra le prix Nobel pour cette découverte.
|
||||
\marginpar{\includegraphics[width=20mm]{Rontgen.jpg}\\première radiographie
|
||||
%"X-ray by Wilhelm Röntgen of Albert von Kölliker's hand - 18960123-01" by Wilhelm Röntgen; originally uploaded to en.wikipedia by E rulez. - Transferred from en.wikipedia.. Licensed under Public domain via Wikimedia Commons - http://commons.wikimedia.org/wiki/File:X-ray_by_Wilhelm_R%C3%B6ntgen_of_Albert_von_K%C3%B6lliker%27s_hand_-_18960123-01.jpg#mediaviewer/File:X-ray_by_Wilhelm_R%C3%B6ntgen_of_Albert_von_K%C3%B6lliker%27s_hand_-_18960123-01.jpg
|
||||
}
|
||||
|
||||
En 1896 il effectuera la première radiographie sur la main d'un de ses collègues.
|
||||
|
||||
\subsection*{1896 : découverte de la radioactivité par Becquerel}
|
||||
Antoine-Henri Becquerel (1852--1928), physicien français, membre dès 1889 de l'Académie des Sciences qu
|
||||
a beaucoup correspondu avec Henri Poincaré, travaille à partir de 1896 sur la fluorescence des sels d'uranium,
|
||||
en conjecturant un phénomène analogue aux rayons X.
|
||||
Un jour il range dans un tiroir, au contact d'une plaque photo, des sels qui n'ont pas été exposés à la lumière.
|
||||
La plaque photo a été impressionée. Il en déduit que ces sels émettent leur propre rayonnement.
|
||||
\marginpar{\includegraphics[width=20mm]{becq.jpg}\\Becquerel
|
||||
%By Nobel foundation [Public domain], via Wikimedia Commons
|
||||
}
|
||||
|
||||
C'est Marie Curie, au cours de sa thèse, qui donnera le nom de \og radioactivité \fg{} à ce phénomène.
|
||||
Elle et Becquerel recevront ensemble le prix Nobel en 1903.
|
||||
|
||||
\subsection*{Marie Curie (1867--1934)}
|
||||
Née à Varsovie, elle entre en Sorbonne en 1891 après que sa ville natale a été annexée par la Russie, qui a interdit aux femmes l'accès l'université.
|
||||
Après avoir épousé en 1894 Pierre Curie, elle commence en 1897 sa thèse sur les rayonnements découverts par Becquerel.
|
||||
\marginpar{\includegraphics[width=20mm]{curie.jpg}\\Marie Curie
|
||||
% "Marie Curie 1903" by Nobel foundation - http://nobelprize.org/nobel_prizes/physics/laureates/1903/marie-curie-bio.html. Licensed under Public domain via Wikimedia Commons - http://commons.wikimedia.org/wiki/File:Marie_Curie_1903.jpg#mediaviewer/File:Marie_Curie_1903.jpg
|
||||
}
|
||||
Elle isole deux nouveaux éléments : le \textbf{polonium} et le \textbf{radium}. Plusieurs tonnes de penchblende sont nécessaires
|
||||
pour un kilogramme de radium.
|
||||
|
||||
Son mari meurt en 1906. Pendant la première guerre mondiale elle crée les premières voitures de radiologie.
|
||||
En 1934 elle décède d'une leucémie. En 1944 L'élément 96 sera baptisé Curium en sa mémoire.
|
||||
|
||||
\subsection*{1900 : Découverte des rayons $\alpha$ et $ \beta $ par Rutherford}
|
||||
Le physicien anglais Ernest Rutherford (1971--1937) identifie le rayons $\alpha$ et $\beta$.
|
||||
Il est considéré comme le père de la physique nucléaire.
|
||||
En 1911 il propose une nouvelle structure de l'atome, opposé au modèle de Thomson : un noyau constitué de charges positives autours duquel évoluent des charges négatives.
|
||||
En 1919 il réussit à voir la première réaction nucléaire : la transformation d'un noyau d'azote en noyau d'oxygène, grâce aux particules $\alpha$.
|
||||
|
||||
%"Ernest Rutherford 1908" by Bain News Service, publisher - This image is available from the United States Library of Congress's Prints and Photographs division under the digital ID ggbain.03392.This tag does not indicate the copyright status of the attached work. A normal copyright tag is still required. See Commons:Licensing for more information.العربية | čeština | Deutsch | English | español | فارسی | suomi | français | magyar | italiano | македонски | മലയാളം | Nederlands | polski | português | русский | slovenčina | slovenščina | Türkçe | 中文 | 中文(简体) | 中文(繁體) | +/−. Licensed under Public domain via Wikimedia Commons - http://commons.wikimedia.org/wiki/File:Ernest_Rutherford_1908.jpg#mediaviewer/File:Ernest_Rutherford_1908.jpg
|
||||
\marginpar{\includegraphics[width=2cm]{ruther.jpg}\\Rutherford}
|
||||
|
||||
\subsection*{1904 : René Blondlot et les rayons N}
|
||||
En 1904, René Blondlot (1849--1930), physicien nancéen reconnu, croit découvrir des rayons qu'il appelle rayons N en référence
|
||||
à sa ville de Nancy. Il s'agit de l'une des plus grandes erreurs expérimentales du xx\textsuperscript{e} siècle : ces rayons n'existent pas,
|
||||
mais, de bonne foi, il réussit à persuader ses collègues, et reçoit un prix de l'Académie des Sciences.
|
||||
|
||||
Cependant en 1905 un Américain, Robert Wood, visite son laboratoire et enlève ce qui est supposé créer les rayons N : les mêmes résultats
|
||||
sont observés.
|
||||
|
||||
\subsection*{1905 : Albert Einstein et l'\og année miraculeuse de la physique \fg{}}
|
||||
|
||||
%« Albert Einstein (Nobel) » par Inconnu — Official 1921 Nobel Prize in Physics photograph. Sous licence Public domain via Wikimedia Commons - http://commons.wikimedia.org/wiki/File:Albert_Einstein_(Nobel).png#mediaviewer/File:Albert_Einstein_(Nobel).png
|
||||
\marginpar{\includegraphics[width=2cm]{einstein.png}\\Einstein}
|
||||
Au début du xx\textsuperscript{e} siècle, Albert Einstein (1879--1955), qui ne
|
||||
trouve pas de poste à l'université,
|
||||
obtient en 1902 un travail à l'office des brevets de Bern en Suisse.
|
||||
En 1905 il publie quatre articles très importants :
|
||||
\begin{description}
|
||||
\item[Mars 1905 :] Publication d'un article sur l'effet photovoltaïque ;
|
||||
\item[Mai 1905 :] Article sur le mouvement brownien (preuve théorique de l'existence des atomes) ;
|
||||
\item[Juin 1905 : ] Bases de la relativité restreinte ;
|
||||
\item[Septembre 1905: ] $E = mc^{2}$.
|
||||
\end{description}
|
||||
|
||||
En 1913 il est nommé à l'Académie des Sciences de Prusse. Il milite en 1914 contre la guerre.
|
||||
Il établit la théorie de la relativité générale en 1915. En 1933 il quitte l'Allemagne pour les États-Unis.
|
||||
Sa lettre à Roosevelt est envoyée en août 1939.
|
||||
Il meurt là-bas d'un rupture d'anévrisme.
|
||||
|
||||
\subsection*{1938 : fission de l'uranium, Hahn et Meitner}
|
||||
Otto Hahn et Lise Meitner réalisent la fission de l'uranium en 1938.
|
||||
%« Otto Hahn und Lise Meitner » par Inconnu — Search + 558596 • Pioneering atomic physicist Ernest Rutherford in his laboratory, ca. 1925. OPA at National ArchivesLise Meitner and Otto Hahn, Kaiser-Wilhelm Institute, Berlin • "...the National Archives identifies the man as Ernest Rutherford, but other sources agree in labeling this a picture of Meitner and Hahn...". The U.S. DOE Office of History. Sous licence Public domain via Wikimedia Commons - https://commons.wikimedia.org/wiki/File:Otto_Hahn_und_Lise_Meitner.jpg#mediaviewer/File:Otto_Hahn_und_Lise_Meitner.jpg
|
||||
\marginpar{\includegraphics[width=2cm]{meitner.jpg}\\Meitner et Hahn}
|
||||
|
||||
|
||||
\subsection*{1939 : détection des neutrons de la fission, Joliot et Curie}
|
||||
En janvier 1939, Frédéric Joliot et Irène Curie (la fille de Marie) détectent les neutrons émis par la fission de l'uranium,
|
||||
ce qui rend possible une réaction en chaîne. Ils calculent la masse critique.
|
||||
Joliot, directeur du CNRS, est un des créateur du CEA.
|
||||
%« Irène et Frédéric Joliot-Curie 1935 » par Agence de presse Meurisse — Bibliothèque nationale de France. Sous licence Public domain via Wikimedia Commons - https://commons.wikimedia.org/wiki/File:Ir%C3%A8ne_et_Fr%C3%A9d%C3%A9ric_Joliot-Curie_1935.jpg#mediaviewer/File:Ir%C3%A8ne_et_Fr%C3%A9d%C3%A9ric_Joliot-Curie_1935.jpg
|
||||
\marginpar{\includegraphics[width=2cm]{joliot.jpg}\\Joliot et Curie}
|
||||
|
||||
|
||||
|
||||
\subsection*{1941 : lancement du projet Manhattan}
|
||||
Avec l'entrée en guerre des États-Unis est lancée le projet Manhattan.
|
||||
En 1942, Groves (militaire) et Oppenheimer (physicien) seront à la tête du projet Manhattan,
|
||||
sur lequel travailleront 300 000 personnes en 1945.
|
||||
|
||||
\subsection*{1942 : première réaction en chaîne, Szilard et Fermi}
|
||||
Léo Szilard (1898--1964) a eu l'idée dès 1933 de la réaction en chaîne, qu'il
|
||||
réussit à effectuer avec Enrico Fermi (1901--1954) en 1942.
|
||||
%« Enrico Fermi 1943-49 » par Department of Energy. Office of Public Affairs — Ce média est disponible dans le catalogue de la National Archives and Records Administration sous l’identifiant ARC (National Archives Identifier) 558578Ce bandeau n’indique rien sur le statut de l’œuvre au regard du droit d'auteur. Un bandeau de droit d’auteur est requis. Voir Commons:À propos des licences pour plus d’informations.English | Español | Français | Italiano | Македонски | മലയാളം | Nederlands | Polski | Português | Русский | Slovenščina | Türkçe | Tiếng Việt | 中文(简体) | 中文(繁體) | +/−. Sous licence Public domain via Wikimedia Commons - http://commons.wikimedia.org/wiki/File:Enrico_Fermi_1943-49.jpg#mediaviewer/File:Enrico_Fermi_1943-49.jpg
|
||||
\marginpar{\includegraphics[width=2cm]{fermi.jpg}\\Fermi}
|
||||
|
||||
La pile de Fermi, réalisée à Chicago cette année-là, est la première centrale productrice d'électricité.
|
||||
|
||||
\subsection*{6 août 1945 : Hiroshima}
|
||||
La bombe \textit{Little Boy}, à base de $^{235}U$, transportée par Paul Tibbets dans son avion
|
||||
\textit{Enola Gay}, fait 70 000 morts immédiats, et 140 000 morts au total.
|
||||
|
||||
\subsection*{9 août 1945 : Nagasaki}
|
||||
%« Nagasakibomb » par The picture was taken by Charles Levy from one of the B-29 Superfortresses used in the attack. — http://www.archives.gov/research/military/ww2/photos/images/ww2-163.jpg National Archives image (208-N-43888). Sous licence Public domain via Wikimedia Commons - http://commons.wikimedia.org/wiki/File:Nagasakibomb.jpg#mediaviewer/File:Nagasakibomb.jpg
|
||||
\marginpar{\includegraphics[width=2cm]{naga.jpg}\\Nagasaki}
|
||||
La bombe composée d'un cœur en plutonium entouré d'explosif fait 40 000 morts immédiats.
|
||||
|
||||
\subsection*{15 août 1945 : capitulation du Japon}
|
||||
|
||||
\subsection*{1948 : Zoé, première pile française}
|
||||
|
||||
\subsection*{1951 : premier réacteur industriel aux États-Unis}
|
||||
|
||||
\subsection*{1952 : explosion de la bombe H}
|
||||
La bombe H s'appuie sur la fusion de l'hydrogène.
|
||||
Sa première explosion a eu lieu sur l'atoll de Bikini en 1952.
|
||||
Son avantage est de ne créer que peu de déchets nucléaires.
|
||||
\subsection*{1954 : premier réacteur industriel en URSS}
|
||||
|
||||
\subsection*{1956 : première centrale française à Marcoule}
|
||||
%http://fresques.ina.fr/reperes-mediterraneens/fiche-media/Repmed00304/le-centre-atomique-de-marcoule.html
|
||||
\marginpar{\includegraphics[width=2cm]{marcoule.eps}\\Centrale de Marcoule
|
||||
}
|
||||
|
||||
\subsection*{1974 : la France choisit le nucléaire}
|
||||
La France décide alors de construire treize nouvelles centrales.
|
||||
|
||||
\subsection*{1980 : utilisation de l'IRM}
|
||||
%« Modern 3T MRI » par User:KasugaHuang — Photographed by User:KasugaHuang on Mar 27, 2006 at Tri-Service General Hospital, Taiwan.. Sous licence Creative Commons Attribution-Share Alike 3.0 via Wikimedia Commons - http://commons.wikimedia.org/wiki/File:Modern_3T_MRI.JPG#mediaviewer/File:Modern_3T_MRI.JPG
|
||||
\marginpar{\includegraphics[width=2cm]{irm.jpg}\\IRM
|
||||
}
|
||||
|
||||
\subsection*{1986 : accident de Tchernobyl}
|
||||
|
||||
|
||||
\subsection*{De nos jours}
|
||||
En 2005 le monde compte 440 réacteurs nucléaires en fonctionnement, dont 59 pour la France,
|
||||
répartis dans 19 centrales, qui ont chacune une puissance de près d'un GW, ce qui représente
|
||||
pour la France 80\% de l'électricité produite.
|
||||
|
||||
En mars 2011 a lieu l'accident de la centrale de Fukushima.
|
||||
|
||||
277
2_rr.tex
Normal file
|
|
@ -0,0 +1,277 @@
|
|||
\part{Relativité restreinte}
|
||||
\paragraph{}
|
||||
|
||||
La relativité \textbf{restreinte} s'appelle ainsi car elle ne s'applique qu'en l'absence
|
||||
de gravitation, et, plus généralement, d'accélération.
|
||||
|
||||
En revanche, la relativité \textbf{générale} est valable en présence de gravitation.
|
||||
|
||||
\section{Composition des vitesses dans la mécanique classique}
|
||||
\subsection{Transformation de Galilée}
|
||||
\paragraph{}
|
||||
|
||||
Un voyageur marche à 5 km/h dans un wagon qui se déplace lui-même à 100 km/h par rapport aux rails.
|
||||
On considère alors deux systèmes $S$ et $S'$ :
|
||||
|
||||
\paragraph{}
|
||||
|
||||
\begin{tabular}{|c|c|c|c|}
|
||||
\hline
|
||||
Premier système de référence & $S$ & attaché aux rails & horloge $H \to t$ \\
|
||||
\hline
|
||||
Deuxième système de référence & $S'$ & attaché au wagon & horloge $H' \to t'$ \\
|
||||
\hline
|
||||
\end{tabular}
|
||||
|
||||
\paragraph{}
|
||||
|
||||
$S'$ est en translation rectiligne uniforme par rapports à $S$. Donc $S'$ et $S$ sont tous deux des référentiels \textbf{inertiels} ou \textbf{galiléens}.
|
||||
|
||||
\paragraph{}
|
||||
|
||||
Soit $w'$ la vitesse du voyageur par rapport au wagon.
|
||||
Pour mesurer cette vitesse,
|
||||
un observateur lié à $S'$ mesure la distance $\Delta x'$
|
||||
parcourue par le voyageur pendant l'intervalle de temps
|
||||
$\Delta t'$.
|
||||
|
||||
Ainsi $w' = \frac{\Delta x'}{\Delta t'} = 5 \textrm{ km/h}$.
|
||||
|
||||
\paragraph{}
|
||||
|
||||
Soit $v$ la vitesse du train par rapport aux rails, et $w$ celle
|
||||
du voyageur par rapport aux rails.
|
||||
Un observateur lié à S' fait la mesure :
|
||||
$w = \frac{\Delta x}{\Delta t} = 105 \textrm{ km/h}$ .
|
||||
|
||||
On a bien : $w = v + w'$, où :
|
||||
\begin{tabular}{|c|c|}
|
||||
\hline
|
||||
$w$ & vitesse absolue \\
|
||||
\hline
|
||||
$v$ & vitesse d'entraînement \\
|
||||
\hline
|
||||
$w'$ & vitesse relative \\
|
||||
\hline
|
||||
\end{tabular}
|
||||
|
||||
\paragraph{}
|
||||
|
||||
Il s'agit de la loi de composition des vitesses en mécanique classique, ou
|
||||
\textbf{transformation de Galilée}.
|
||||
Le temps y est absolu : $t=t'$.
|
||||
|
||||
\subsection{Problème de la vitesse de la lumière}
|
||||
\paragraph{}
|
||||
|
||||
Que se passe-t-il pour la lumière ?
|
||||
Considérons $P$, position d'un flash lumineux qui se propage.
|
||||
Un observateur lié à $S'$ mesure la vitesse
|
||||
$w' = \frac{\Delta x'}{\Delta t'} = c =$ 299 792 458 m/s.
|
||||
Un autre observateur, lié à $S$, mesure
|
||||
$w =\frac{\Delta x}{\Delta t} = c$, soit la même vitesse !
|
||||
|
||||
Cette fois
|
||||
$w \neq v + w' $ :
|
||||
\textbf{la loi de transformation galiléenne ne s'applique plus.}
|
||||
|
||||
\paragraph{}
|
||||
|
||||
En réalité, la constance de $c$, vitesse de la lumière dans le vide,
|
||||
quel que soit le référentiel a été
|
||||
démontrée en 1887 par l'expérience de Michelson et Morley,
|
||||
expérience confirmée par la suite.
|
||||
|
||||
\section{Composition des vitesses en relativité restreinte}
|
||||
\subsection{Postulats}
|
||||
\paragraph{}
|
||||
|
||||
\textbf{Deuxième postulat de la relativité restreinte :} la vitesse
|
||||
de la lumière ne présente jamais de valeur relative.
|
||||
Dans le vide (ou dans l'air) cette vitesse est égale à $c$ dans
|
||||
tous les référentiels d'inertie.
|
||||
|
||||
\paragraph{}
|
||||
|
||||
Or $c = \frac{d}{t}$. Il faut donc trouver un nouvelle loi d'addition des vitesse.
|
||||
|
||||
\paragraph{}
|
||||
|
||||
\textbf{Premier postulat de la relativité restreinte :}
|
||||
les lois de la physique sont les mêmes dans tous les référentiels d'inertie.
|
||||
|
||||
\subsection{Cas particulier : $x' = 0$}
|
||||
\paragraph{Cadre de l'étude}
|
||||
|
||||
On reprend l'exemple précédent, avec les référentiels $S$ et $S'$ :
|
||||
$Ox'$ a un mouvement rectiligne parallèle à $Ox$,
|
||||
de vitesse constante $v$ par rapport à $S$. $S$ et $S'$ sont donc
|
||||
toujours des référentiels d'inertie.
|
||||
|
||||
\paragraph{Introduction de $\gamma$}
|
||||
|
||||
Soit $P$ la position d'un point quelconque, repéré en $S$ par $x$,
|
||||
et en $S'$ par $x'$. Un horloge dans $S$ donne le temps $t$,
|
||||
une autre dans $S'$ donne le temps $t'$.
|
||||
|
||||
À $t=t'=0$ on considère que $O \equiv O'$.
|
||||
Ainsi, $x'=0 \Rightarrow O \equiv O'$. Dans le cas où $x'=0$, on a alors $x=x_{0}=vt$,
|
||||
en effet $O'$ caractérise le mouvement de $S$ par rapport à $S'$.
|
||||
|
||||
On suppose que $x'$ est une fonction polynomiale en $x$.
|
||||
Alors, comme $x'_{(x=x_{0})}=0$, $x'$ admet $(x-x_{0})$ en facteur.
|
||||
Donc il existe $\gamma$ fonction polynomiale en $x$ telle que : $ x' = \gamma (x - x_{0})$.
|
||||
D'où :
|
||||
%\begin{figure}
|
||||
%\begin{empheq}[box=\fbox]{equation}
|
||||
\begin{equation}
|
||||
\boxed{x' = \gamma (x - vt)}
|
||||
\label{EQI}
|
||||
\end{equation}
|
||||
%\end{empheq}
|
||||
%\end{figure}
|
||||
|
||||
\subsection{Calcul de $\gamma$}
|
||||
\paragraph{}
|
||||
|
||||
En mécanique classique, $\gamma = 1$. Mais que vaut $\gamma$ dans le cas de la relativité restreinte ?
|
||||
Utilisons le postulat que $c \equiv constante$.
|
||||
|
||||
\paragraph{}
|
||||
|
||||
Soit $P$ un point lumineux émis à $t = t' = 0$ en $O \equiv O'$. On a alors :
|
||||
\begin{equation}
|
||||
\textrm{ dans } S' : x' = c t'
|
||||
\label{S'}
|
||||
\end{equation}
|
||||
\begin{equation}
|
||||
\textrm{ dans } S : x = c t
|
||||
\label{S}
|
||||
\end{equation}
|
||||
|
||||
\paragraph{}
|
||||
|
||||
Plutôt qu'une relation du type $x' = f(x, t)$, on voudrait établir une relation de la forme $t' = f(t, x)$.
|
||||
On cherche alors $a$ et $b$ tels que :
|
||||
\begin{equation}
|
||||
t' = at + bx
|
||||
\label{eq*}
|
||||
\end{equation}
|
||||
|
||||
L'équation (\ref{EQI}) donne alors :
|
||||
\[
|
||||
\textrm{(\ref{EQI})}
|
||||
\underset{\textrm{(\ref{S})}}{\Rightarrow}
|
||||
x' = \gamma \left(ct - v\frac{x}{c}\right)
|
||||
\underset{\textrm{(\ref{S'})}}{\Rightarrow}
|
||||
ct' = \gamma \left(ct - v\frac{x}{c}\right)
|
||||
\underset{ \textrm{(\ref{eq*})}}{\Rightarrow}
|
||||
c(at + bx) = \gamma \left(ct - v \frac{x}{c}\right)
|
||||
\]
|
||||
|
||||
D'où, par identification, $a = \gamma$ et $b = - \frac{\gamma v}{c^{2}}$.
|
||||
|
||||
\paragraph{}
|
||||
|
||||
Ainsi, d'après (\ref{eq*}),
|
||||
%\begin{empheq}[box=\fbox]{equation}
|
||||
\begin{equation}
|
||||
\boxed{
|
||||
t' = \gamma \left(t - \frac{v}{c^{2}}x \right)
|
||||
}
|
||||
\label{EQII}
|
||||
\end{equation}
|
||||
%\end{empheq}
|
||||
|
||||
Or la vitesse $v$ est relative aux deux systèmes :
|
||||
$S'$ est en droit de se considérer au repos
|
||||
et de voir $S$ se déplacer par rapport à lui
|
||||
avec la vitesse $-v$.
|
||||
C'est le principe de réciprocité des vitesses.
|
||||
On a alors, en supposant que $\gamma(-v) = \gamma(v)$ :
|
||||
\begin{equation}
|
||||
x = \gamma \left(x' + v t' \right)
|
||||
\label{EQI'}
|
||||
\end{equation}
|
||||
\begin{equation}
|
||||
t = \gamma \left(t' + \frac{v}{c^{2}} x' \right)
|
||||
\label{EQII'}
|
||||
\end{equation}
|
||||
|
||||
Ainsi, (\ref{EQI}) s'écrit :
|
||||
\[
|
||||
x' = \gamma (x - vt)
|
||||
\underset{\textrm{(\ref{EQI'}) et (\ref{EQII'})}}{=}
|
||||
\gamma^{2} x' \left( 1 - \frac{v^{2}}{c^{2}} \right)
|
||||
\]
|
||||
|
||||
Cela est vrai pour tout $x' \neq 0$, d'où
|
||||
$1 = \gamma^{2} (1 - \frac{v^{2}}{c^{2}})$.
|
||||
Ainsi :
|
||||
\begin{equation}
|
||||
\boxed{
|
||||
\gamma = \frac{1}{\sqrt{1-\frac{v^{2}}{c^{2}}}}
|
||||
}
|
||||
\label{eqgamma}
|
||||
\end{equation}
|
||||
|
||||
On observe que $\gamma$ est paire en $v$,
|
||||
ce qui est cohérent avec l'hypothèse qui nous a permis d'écrire
|
||||
les équations (\ref{EQI'}) et (\ref{EQII'}).
|
||||
|
||||
\paragraph{Conclusion}
|
||||
|
||||
\begin{itemize}
|
||||
\item
|
||||
Si $v \ll c$, alors
|
||||
$\gamma \approx 1$ et on retrouve la transformation galiléenne.
|
||||
\item
|
||||
Sinon, $\gamma \neq 1$,
|
||||
et on doit appliquer une \textbf{transformation de Lorentz.}
|
||||
\end{itemize}
|
||||
|
||||
\subsection{Composition des vitesses}
|
||||
\paragraph{}
|
||||
|
||||
Maintenant, considérons $P$ animé d'une vitesse $w'$ par rapport à $S'$.
|
||||
|
||||
\[ x' = w' t' \]
|
||||
\[ \underset{\textrm{(\ref{EQI}) et (\ref{EQII})}}{\Rightarrow} \gamma (x - vt) = w' \gamma \left( t - \frac{v}{c^{2}}x \right) \]
|
||||
\[ \Rightarrow x \left( 1 + w' \frac{v}{c^{2}} \right) = t ( w' + v ) \]
|
||||
|
||||
Or $w$ vitesse de $P$ par rapport à $S$ vérifie $x=wt$, d'où la \textbf{nouvelle loi de composition des vitesses}
|
||||
\begin{equation}
|
||||
\boxed{
|
||||
w = \frac{w' + v}{1 + w' \frac{v}{c^{2}} }
|
||||
}
|
||||
\label{eqcompos}
|
||||
\end{equation}
|
||||
|
||||
\paragraph{Cas particuliers}
|
||||
|
||||
\begin{itemize}
|
||||
\item
|
||||
Si $w' \ll c$ et $v \ll c$ alors $w \approx w' + v$ (transformation de Galilée) ;
|
||||
\item
|
||||
si $w' = c$ alors $w = c$ ;
|
||||
\item
|
||||
de même, si $v = c$ alors $w = c$.
|
||||
\end{itemize}
|
||||
|
||||
\begin{figure}
|
||||
\centering
|
||||
\includegraphics[width=10cm]{relat.eps}
|
||||
\caption{$w = f(w')$, cf. eq (\ref{eqcompos}), pour $v = 1 \times 10^{8}$ m/s, d'après les transformations de Galilée (trait fin) et de Lorentz (trait large)}
|
||||
|
||||
% code Maxima utilisé pour réaliser le graphe :
|
||||
|
||||
% f(w,v,c):=(w+v)/(1+w*(v/c**2));c:3*10**8;v:1*10**8;
|
||||
|
||||
% relat(x):=f(x,v,c);galil(x):=x+v;
|
||||
|
||||
% plot2d ([relat(w),galil(w),c],[w, 0, 3*10**8],[y, 0, 4*10**8],[gnuplot_term,ps],[gnuplot_out_file,"relat.eps"],
|
||||
% [xlabel, "w' (m/s)"],[ylabel, "w (m/s)"], [style, [lines,4,5],[lines,2,5],[lines,0.5,5]],[legend,false]);
|
||||
|
||||
\label{f(w')}
|
||||
\end{figure}
|
||||
|
||||
278
3_rr2.tex
Normal file
|
|
@ -0,0 +1,278 @@
|
|||
% cours numéro 3
|
||||
|
||||
|
||||
\section{Conséquences}
|
||||
\subsection{Deux évènements}
|
||||
\paragraph{}
|
||||
On considère deux évènements, repérés,
|
||||
\begin{itemize}
|
||||
\item
|
||||
dans $S$, par $(x_{1}, t_{1})$ et $(x_{2}, t_{2})$ ;
|
||||
\item
|
||||
dans $S'$, par $(x'_{1}, t'_{1})$ et $(x'_{2}, t'_{2})$.
|
||||
\end{itemize}
|
||||
|
||||
\paragraph{}
|
||||
On définit alors les durées et les distances :
|
||||
\begin{itemize}
|
||||
\item
|
||||
$\Delta x = x_{2} -x_{1}$
|
||||
\item
|
||||
$\Delta t = t_{2} -t_{1}$
|
||||
\item
|
||||
$\Delta x' = x'_{2} - x'_{1}$
|
||||
\item
|
||||
$\Delta t' = t'_{2} -t'_{1}$
|
||||
\end{itemize}
|
||||
|
||||
\paragraph{}
|
||||
D'après \eqref{EQI}, on a
|
||||
\begin{equation}
|
||||
\Delta x' = \gamma \left( \Delta x -v \Delta t \right)
|
||||
\label{eq3}
|
||||
\end{equation}
|
||||
|
||||
De même, d'après \eqref{EQII}, on a aussi
|
||||
\begin{equation}
|
||||
\Delta t' = \gamma \left(\Delta t - \frac{v}{c^{2}} \Delta x \right)
|
||||
\label{eq4}
|
||||
\end{equation}
|
||||
|
||||
|
||||
\subsection{Contraction des longueurs}
|
||||
\paragraph{}
|
||||
Soit un corps de longueur $\Delta x$ dans $S$, $\Delta x'$ dans $S'$.
|
||||
On fait une photo à un instant $t=t_{1}=t_{2}$. On a $\Delta x = x_{2}- x_{1}$.
|
||||
Ainsi, d'après \eqref{eq3}, avec $\Delta t = 0$ :
|
||||
\[
|
||||
\boxed{
|
||||
\Delta x' = \gamma \Delta x = \frac{\Delta x}{ \sqrt{ 1 - \frac{v^{2}}{c^{2}} }}
|
||||
}
|
||||
\]
|
||||
|
||||
Au final on obtient $\Delta x' > \Delta x $ : un objet qui mesure $\Delta x'$ dans $S'$ paraît contracté dans $S$.
|
||||
|
||||
\subsection{Dilatation des durées}
|
||||
\paragraph{}
|
||||
D'après \eqref{eq4}, par symétrie,
|
||||
\begin{equation}
|
||||
\Delta t = \gamma \left(\Delta t' + \frac{v}{c^{2}} \Delta x' \right)
|
||||
\label{eq4'}
|
||||
\end{equation}
|
||||
|
||||
\paragraph{}
|
||||
Pour deux évènements localisés au même endroit dans $S'$, on a $x'=x'_{1}=x'_{2}$ donc $\Delta x' = 0$.
|
||||
Ainsi \eqref{eq4'} donne :
|
||||
\[
|
||||
\boxed{
|
||||
\Delta t = \gamma \Delta t' = \frac{\Delta t'}{\sqrt{1-\frac{v^{2}}{c^{2}}}}
|
||||
}
|
||||
\]
|
||||
|
||||
D'où au final $\Delta t > \Delta t' $ : il y a dilatation des durées pour l'observateur en $S$ ;
|
||||
on parle de \og retard \fg{} des horloges mobiles, retard qui a pu être observé sur les horloges des avions.
|
||||
|
||||
\paragraph{Exemple des muons}
|
||||
Un autre exemple de ce phénomène concerne les muons qui pénètrent dans l'atmosphère avec une vitesse très élevée : le temps perçu par les muons n'est pas le même que celui que nous percevons.
|
||||
% schéma 2
|
||||
|
||||
\paragraph{Paradoxe des jumeaux de Langevin}
|
||||
On considère deux jumeaux, A et B. A reste sur la Terre, alors que B voyage avec la vitesse $v$ à travers l'espace. On pose $v$ = 0,99 c.
|
||||
|
||||
D'après la relativité restreinte, si pour l'horloge de A, la durée du voyage est de $\Delta t =$ 14 ans,
|
||||
pour l'horloge de B, cette durée n'a été que de $\Delta t' \approx$ 2 ans.
|
||||
|
||||
Ainsi, pendant que le voyageur B a vieilli de deux ans, A a vieilli de 14 ans. Mais, au retour de B, sera-t-il réellement plus jeune que A ?
|
||||
|
||||
Un aller-retour nécessite des accélérations : des changements de vitesse. Donc la relativité restreinte ne s'applique plus. Il faut faire appel à la relativité générale pour répondre à cette question.
|
||||
|
||||
\paragraph{Exemple du train}
|
||||
Un observateur est fixe dans $S'$, référentiel lié au wagon.
|
||||
% schéma 3 i
|
||||
Il considére l'horloge suivante : entre 2 miroirs, séparés par une longueur $L$, un photon fait des aller-retours.
|
||||
Chacun de ces aller-retours correspond à une période de l'horloge :
|
||||
$\Delta t' = \frac{2L}{c} = \frac{d'}{c}$, où $ d' = 2L $.
|
||||
|
||||
Cette fois l'observateur est fixe dans $S$, référentiel lié aux rails.
|
||||
Le wagon est en translation à la vitesse $v$ par rapport à $S$.
|
||||
% schéma 3 ii
|
||||
L'observateur mesure $\Delta t = \frac{d}{c}$
|
||||
|
||||
Or on a $ d > d' = 2L $, donc on a aussi $\Delta t > \Delta t'$.
|
||||
|
||||
\section{Équivalence Masse-Énergie}
|
||||
\subsection{Énergies totales et quantités de mouvement}
|
||||
\paragraph{}
|
||||
|
||||
On considère un corps en mouvement de translation rectiligne uniforme de vitesse quelconque
|
||||
par rapport à $S'$.
|
||||
|
||||
Si on lui applique une force $F$ sur une distance $\Delta x'$, son énergie varie de $\Delta E' = F\Delta x'$. Ainsi :
|
||||
\[ \Delta x' = \frac{\Delta E'}{F}\]
|
||||
|
||||
On se place maintenant dans $S$.
|
||||
Or, d'après le premier postulat, la force $F$ est invariante : $F \equiv F'$.
|
||||
On a donc aussi :
|
||||
\[ \Delta x = \frac{\Delta E}{F} \]
|
||||
|
||||
\paragraph{}
|
||||
|
||||
De même, pour la quantité de mouvement, d'après le PFD,
|
||||
$F = \frac{\Delta p}{\Delta t} = \frac{\Delta p'}{\Delta t'}$,
|
||||
donc :
|
||||
\[ \Delta t = \frac{\Delta p}{F} \textrm{ et } \Delta t' = \frac{\Delta p'}{F} \]
|
||||
|
||||
On porte ces longueurs et ces dureés dans \eqref{eq3} et \eqref{eq4}.
|
||||
|
||||
Alors
|
||||
$\frac{\Delta E'}{F} = \gamma ( \frac{\Delta E}{F} - v \frac{\Delta p}{F})$,
|
||||
donc on obtient finalement :
|
||||
\[ \Delta E' = \gamma ( \Delta E - v \Delta p ) \]
|
||||
|
||||
%\newcommand{\D}{\Delta}
|
||||
|
||||
\paragraph{}
|
||||
|
||||
De même, $\frac{\D p'}{F} = \gamma( \frac{\D p}{F} - \frac{v}{c^{2}} \frac{\D E}{F} )$,
|
||||
ainsi on obtient :
|
||||
\[ \D p' = \gamma (\D p - \frac{v}{c^{2}} \D E ) \]
|
||||
|
||||
Après avoir établi les équations symétriques, on obtient en fin de compte :
|
||||
\begin{equation}
|
||||
\boxed{
|
||||
E' = \gamma ( E - vp)
|
||||
}
|
||||
\label{eq5}
|
||||
\end{equation}
|
||||
\begin{equation}
|
||||
\boxed{
|
||||
p' = \gamma (p - \frac{v}{c^{2}} E )
|
||||
}
|
||||
\label{eq6}
|
||||
\end{equation}
|
||||
|
||||
\subsection{Énergies cinétiques}
|
||||
\paragraph{Utilisation d'un cas particulier}
|
||||
|
||||
On utilise un cas particulier : si le corps a une vitesse $v$ par rapport à $S$,
|
||||
il doit être au repos dans $S'$.
|
||||
Alors l'énergie cinétique dans $S$ s'écrit $E'_{c} = 0$, et $p' = 0$.
|
||||
|
||||
On pose l'énergie totale $E' = 0 + E'_{0}$ (somme de l'énergie cinétique et de l'énergie au repos, sorte d'énergie potentielle ou interne).
|
||||
On ne sait pas à quoi elle est égale pour le moment.
|
||||
|
||||
\paragraph{}
|
||||
|
||||
L'équation \eqref{eq5} donne : $0 + E'_{0} = \gamma( E - vp)$.
|
||||
|
||||
L'équation \eqref{eq6} donne :
|
||||
$0 = \gamma ( p - \frac{v}{c^{2}} E) $
|
||||
d'où $p = \frac{v}{c^{2}} E$.
|
||||
|
||||
\paragraph{}
|
||||
|
||||
Ainsi on obtient les relations suivantes :
|
||||
\[ E'_{0} = \gamma \left( E -\frac{v^2}{c^2} E \right) \]
|
||||
|
||||
\begin{equation}
|
||||
E = \frac{E'_{0}}{ \sqrt{1 - \frac{v^2}{c^2}}}
|
||||
\label{eqEE'}
|
||||
\end{equation}
|
||||
|
||||
\begin{equation}
|
||||
p = \frac{v}{c^{2}} \frac{E'_{0}}{ \sqrt{1 - \frac{v^2}{c^2}}}
|
||||
\label{eqp}
|
||||
\end{equation}
|
||||
|
||||
\paragraph{}
|
||||
|
||||
On utilise le fait que, quand $v \ll c$, on doit retrouver la mécanique classique, notamment
|
||||
$p = m_{0} v$, où $m_{0}$ est la masse du corps au repos.
|
||||
|
||||
Or, quand $v \ll c$,
|
||||
\[ p = \frac{v}{c^{2}} \frac{E'_{0}}{ \sqrt{1 - \frac{v^2}{c^2}}} \approx \frac{v}{c^{2}} E'_{0} = m_{0} v \]
|
||||
|
||||
On obtient alors : $E'_{0} = m_{0} c^{2}$.
|
||||
|
||||
Or $E'_{0}$ ne dépend ni de $v$, ni de $w$ ou $w'$, on a donc :
|
||||
\begin{equation}
|
||||
\boxed{
|
||||
E_{0} = E'_{0} = m_{0} c^{2}
|
||||
}
|
||||
\label{eqE0}
|
||||
\end{equation}
|
||||
|
||||
qui est l'énergie du système au repos, l'énergie \og potentielle \fg{} $E_{0}$.
|
||||
|
||||
\paragraph{Masse et vitesse}
|
||||
|
||||
Ainsi, d'après \eqref{eqp} et \eqref{eqE0},
|
||||
$p = \frac{m_{0}}{\sqrt{1 - \frac{v^{2}}{c^{2}}}} v$.
|
||||
|
||||
Donc, en posant :
|
||||
\begin{equation}
|
||||
\boxed{
|
||||
m = \gamma m_{0} = \frac{m_{0}}{ \sqrt{1 - \frac{v^{2}}{c^{2}}} }
|
||||
}
|
||||
\label{eqm}
|
||||
\end{equation}
|
||||
on a bien $p = m v$.
|
||||
|
||||
On observe alors que la masse augmente quand $v$ augmente :
|
||||
$m \rightarrow \infty$ quand $v \rightarrow c$.
|
||||
|
||||
\paragraph{Énergie totale}
|
||||
Par \eqref{eqEE'} et \eqref{eqE0}, on a l'égalité :
|
||||
$E = \gamma m_{0} c^{2}$.
|
||||
Puis, d'après \eqref{eqm}, l'énergie totale s'écrit :
|
||||
\begin{equation}
|
||||
\boxed{
|
||||
E = m c^{2} %% encadrer
|
||||
}
|
||||
\label{eqeneg}
|
||||
\end{equation}
|
||||
|
||||
\paragraph{Énergie cinétique relativiste}
|
||||
|
||||
On a, par définition, $ E = E_{c} + E_{0} $,
|
||||
d'où $ E_{c} = E - E_{0} = m c^{2} - m_{0} c ^{2}$, soit :
|
||||
\begin{equation}
|
||||
\boxed{
|
||||
E_{c} = m_{0} c ^{2} ( \gamma - 1 )
|
||||
}
|
||||
\label{eqEc}
|
||||
\end{equation}
|
||||
|
||||
\paragraph{Cas particulier : lois classiques}
|
||||
Quand $\frac{v}{c} \rightarrow 0$,
|
||||
$ E_{c} \approx m_{0} c ^{2} ( 1 + \frac{v^{2}}{c^{2}} - 1 ) = \frac{1}{2} m_{0} v^{2} $,
|
||||
et on retrouve bien l'$E_{c}$ de la mécanique classique.
|
||||
|
||||
\paragraph{Remarques}
|
||||
\begin{itemize}
|
||||
\item
|
||||
Aux faibles vitesses, l'énergie totale s'écrit : $E \approx m_{0} c^{2} + \frac{1}{2} m_{0} v^{2} $
|
||||
\item
|
||||
Pour le photon, $v = c$, soit $m \rightarrow \infty$ d'après l'équation \eqref{eqm}, mais en fait, $m_{0} = 0$
|
||||
(la masse au \og repos \fg{} du photon est nulle, mais cela ne signifie pas grand chose car un photon est toujours à la vitesse $c$),
|
||||
donc $m = 0$ pour tout $v$.
|
||||
\item
|
||||
on peut écrire l'énergie totale sous la forme $E^{2} = p^{2} c^{2} + m_{0}^{2} c^{4} $
|
||||
\end{itemize}
|
||||
|
||||
\paragraph{Exemple}
|
||||
On considère un proton ($m_{0}= 1,67.10^{-27}$ kg) à la vitesse $v_{1}=$ 299~000 km/h.
|
||||
Alors
|
||||
$E_{c1} =$ 2,45 $10^{-9}$ J = 15,3 GeV
|
||||
et $m_{1} =$ 16,3 $m_{0}$.
|
||||
|
||||
On double son énergie : désormais $E_{c2}=$ 30,6 GeV
|
||||
|
||||
Alors $v_{2}=$ 299 730 km/s
|
||||
et $m_{2}=$ 32,3 $m_{0}$.
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
1166
4_noyau.tex
Normal file
173
5_rp.tex
Normal file
|
|
@ -0,0 +1,173 @@
|
|||
\part{Radioprotection}
|
||||
|
||||
\section{Présentation}
|
||||
\subsection{Radioactivité}
|
||||
|
||||
Un noyau instable (radioactif) subit une transformation pour atteindre une configuration stable.
|
||||
|
||||
Radioactivité :
|
||||
\begin{itemize}
|
||||
\item
|
||||
$\n{\alpha}{4}{2}$
|
||||
\item
|
||||
$\beta$
|
||||
\item
|
||||
$\gamma$ : grains d'énergie (photons), le noyau ne change pas de nature dans ce cas.
|
||||
\end{itemize}
|
||||
|
||||
\subsection{Mesures de la radioactivité}
|
||||
\paragraph{Le Becquerel}
|
||||
|
||||
1 Bq : une désintégration par seconde.
|
||||
|
||||
Mais cette unité ne tient pas compte de la nature du rayon, de son énergie.
|
||||
En effet les particules émises se propagent, elles rencontrent de la matière, et déposent leur énergie, et la matière peut s'échauffer, mais peut aussi être modifiée.
|
||||
Il a donc fallu élaborer d'autre grandeurs et d'autres unités.
|
||||
|
||||
\section{Nouvelles grandeurs utilisées}
|
||||
\subsection{Le Gray}
|
||||
|
||||
Notre organisme est le siège en permanence de destructions et reconstructions cellulaires.
|
||||
Si le rayonnement tue une cellule, peu grave : elle est recréée.
|
||||
Mais si le rayonnement est massif, on aura une liaison massive du tissu cellulaire, et donc une perturbation.
|
||||
Au-delà d'un certain seuil d'irradiation, on a des effets à coup sûr : des \textbf{effets déterministes}
|
||||
Ces effets déterministes (fortes doses d'irradiations) sont mesurés par le \textbf{Gray (gy)}.
|
||||
|
||||
$$ 1 \text{gy} \equiv 1 \text{ Joule absorbé par kg de matière cible} \equiv1 J/kg $$
|
||||
|
||||
\begin{itemize}
|
||||
\item
|
||||
Pour une dose inférieure à 300 mgy, il n'y aucun effet déterministe sur le tissu.
|
||||
\item
|
||||
Pour une dose supérieure à 5 000 mgy ou 5 gy, il y a une chance sur deux de survie.
|
||||
\item
|
||||
Pour une dose supérieure à 15 gy, mort certaine.
|
||||
\end{itemize}
|
||||
|
||||
\subsection{Dose équivalente}
|
||||
\paragraph{Autres formes de dégâts}
|
||||
|
||||
Peut se produire une irradiation de la molécule d'ADN, qui ne provoque pas forcément la mort de la molécule, mais une mutation possible de l'ADN.
|
||||
Le système immunitaire peut certes repérer et réparer cette mutation, mais l'échec est possible.
|
||||
Si cette mutation prolifère, c'est le début d'une cancérisation.
|
||||
La probabilité varie avec la dose reçue : La mutation n'est pas certaine.
|
||||
Il y a donc un \textbf{effet probabiliste ou stochastique}.
|
||||
|
||||
Pour estimer cette probabilité, on tient compte de l'énergie déposée par kg de matière, mais on tient compte également de la nature du rayon (effets biologiques divers).
|
||||
Si on a affaire à des neutrons, on multiplie par 5 à 20 (neutrons à 1 MeV) l'énergie déposée.
|
||||
|
||||
$$ J.kg^{-1} : gy \times \text{ facteur lié au rayon} \Rightarrow \text{Sievert (Sv)} (J.kg^{-1}) $$
|
||||
|
||||
Ces facteurs sont :
|
||||
|
||||
\paragraph{}
|
||||
|
||||
\begin{tabular}{r|| c c c c c }
|
||||
Type d'émission & Photons & $\beta$ & Neutrons & Protons & $\n{\alpha}{4}{2}$ \\
|
||||
\hline
|
||||
Facteur de qualité Q& 1 & 1 & 5 à 20 & 5 à 10 & 20 \\
|
||||
\end{tabular}
|
||||
|
||||
\paragraph{Dose équivalente}
|
||||
|
||||
Cela correspond à la \textbf{dose équivalente}. Son unité est toujours le Sievert.
|
||||
|
||||
\subsection{Dose efficace}
|
||||
|
||||
Cette fois on prend en compte un deuxième facteur correctif, lié à la nature du tissu irradié.
|
||||
C'est la \textbf{dose efficace}.
|
||||
Ce facteur est, par exemple, pour la peau et les os, de 1, alors que pour la moelle osseuse, le colon, ou l'estomac, de 12.
|
||||
|
||||
\section{Risques}
|
||||
|
||||
\subsection{Estimations des risques}
|
||||
|
||||
\begin{itemize}
|
||||
\item
|
||||
Environ 0,005\% par mSv de risque de développer un cancer.
|
||||
\item
|
||||
En dessous de 100 mSv, cette loi surestimerait le risque.
|
||||
\item
|
||||
De 100 à 1000 mSv, les risques de cancer croient régulièrement et sont scientifiquement établis.
|
||||
\item
|
||||
100 mSv : risque de 0,5\%
|
||||
\item
|
||||
1000 mSv : risque de 5\%
|
||||
\item
|
||||
6 Sv : dose mortelle
|
||||
\end{itemize}
|
||||
|
||||
\paragraph{Remarques}
|
||||
|
||||
Sur une population de 100 000 personnes, 20 000 à 25 000 personnes vont développer un cancer (toutes causes confondues).
|
||||
Si cette population est soumise à une irradiation de 100 mSv, on aura (0,005\%/mSv) 500 cas supplémentaires dus à cette irradiation.
|
||||
|
||||
\subsection{Ordres de grandeur}
|
||||
\begin{itemize}
|
||||
\item
|
||||
2 mSv : dose de radioactivité terrestre reçue par an (Uranium, Potassium, Radon) ;
|
||||
\item
|
||||
0,4 mSv : radioactivité due aux rayonnements cosmiques ($\n{C}{14}{}$, Tritium) ;
|
||||
\item
|
||||
0,3 mSv : radio des poumons (rayons X) ;
|
||||
\item
|
||||
0,1 mSv : voyage en avion, voyage en altitude ;
|
||||
\item
|
||||
un scanner : jusqu'à 10 mSv ;
|
||||
\item
|
||||
travailleurs du nucléaire : plafond de 100 mSv sur 5 ans, sans dépasser 50 mSv en un an.
|
||||
\end{itemize}
|
||||
|
||||
\subsection{Exemples}
|
||||
\subsubsection{Tchernobyl}
|
||||
Bilan 15 ans après la catastrophe : 44 morts rapides et 234 cas d'irradiation à forte dose. Pour les liquidateurs (population de 600 000 personnes) : de 10 à 500 mSv (à peu près 1\% de cancers en excès attendus).
|
||||
Pour la population : 135 000 habitants proches évacués. 10 mSv, et 0,1\% de cancers en plus.
|
||||
Pour les 3 700 000 personnes vivant dans des zones légèrement contaminées : 7 mSv/an en moyenne.
|
||||
|
||||
\subsubsection{Fukushima (12.03.2011)}
|
||||
|
||||
14.03.2011 : 167 Sv/h au niveau du réacteur (enceinte de confinement)
|
||||
|
||||
3.04.2011 : à 5 km de la centrale, 112$\mu$Sv/h
|
||||
|
||||
167 travailleurs de Tepco ont reçu des doses supérieures à 100 mSv
|
||||
|
||||
Villes alentours : entre 10 et 50 mSv. Jusqu'àa 30 km de la centrale, entre 100 et 200 mSv parfois observés.
|
||||
|
||||
%Rayons X, $\gamma$, ondes électromagnétiques ($\lambda < 0,1 \mu\text{m}$), $\n{\alpha}{4}{2}$, $\beta$, neutrons : rayonnements ionisants (H $\rightarrow$ 13,6 eV)
|
||||
% ??
|
||||
|
||||
|
||||
|
||||
\section{Comment se protéger ?}
|
||||
Trois mots-clés :
|
||||
Distance, Temps, Écrans.
|
||||
|
||||
\subsection{Écrans}
|
||||
|
||||
\begin{itemize}
|
||||
\item
|
||||
$\alpha$ : arrêtés par une feuille de papier ;
|
||||
\item
|
||||
$\beta$ : feuille de métal ;
|
||||
\item
|
||||
$\gamma$ : plusieurs cm de plomb ;
|
||||
\item
|
||||
neutrons : importante épaisseur de béton, d'eau ou de paraffine.
|
||||
\end{itemize}
|
||||
|
||||
\section{Déchets nucléaires liés à la fission}
|
||||
|
||||
En France, 1 kg de déchet nucléaire par habitant et par an est produit.
|
||||
Sur ce kilogramme, 990 grammes dont la période est inférieure à 300 ans.
|
||||
Il reste 10 grammes qui ont une durée de vie très longue, ce sont les plus préoccupants.
|
||||
Cela représente 600 tonnes par an.
|
||||
|
||||
La France possède un cycle ouvert : on traite les déchets (retraitement) en séparant les différents constituants chimiquement.
|
||||
Dans une tonne de combustible usé (après 3 ans dans un REP), l'Uranium est présent à 95,3\% et le Plutonium est présent à 1\%. Ces éléments-là sont valorisables.
|
||||
Les produits de fissions représentent 3,7\%.
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
6
6_plasma.tex
Normal file
|
|
@ -0,0 +1,6 @@
|
|||
\part{Plasmas}
|
||||
|
||||
paramètre de grain :
|
||||
|
||||
$ g \ll 1 $ : énergie coulombienne très inférieure à l'énergie thermique
|
||||
|
||||
BIN
Klaproth.jpg
Normal file
|
After 
(image error) Size: 554 KiB |
BIN
Otto_Hahn_und_Lise_Meitner.jpg
Normal file
|
After 
(image error) Size: 2 MiB |
BIN
Pichblende.jpg
Normal file
|
After 
(image error) Size: 27 KiB |
BIN
Rontgen.jpg
Normal file
|
After 
(image error) Size: 24 KiB |
39
annexe.tex
Normal file
|
|
@ -0,0 +1,39 @@
|
|||
\part{Annexe}
|
||||
|
||||
\begin{figure}
|
||||
\centering
|
||||
\caption{Plan du cours}
|
||||
\includegraphics[width=15cm]{plan3.png}
|
||||
\end{figure}
|
||||
|
||||
|
||||
\begin{figure}
|
||||
\centering
|
||||
\caption{Tableau périodique des éléments}
|
||||
\includegraphics[width=15cm]{tabper2.png}
|
||||
\end{figure}
|
||||
|
||||
|
||||
\begin{figure}
|
||||
\centering
|
||||
\caption{Feuillo d'exercices recto}
|
||||
\includegraphics[width=15cm]{exo1.png}
|
||||
\end{figure}
|
||||
|
||||
\begin{figure}
|
||||
\centering
|
||||
\caption{Feuillo d'exercices verso}
|
||||
\includegraphics[width=15cm]{exo22.png}
|
||||
\end{figure}
|
||||
|
||||
\begin{figure}
|
||||
\centering
|
||||
\caption{Correction des exercices recto}
|
||||
\includegraphics[width=15cm]{correc.png}
|
||||
\end{figure}
|
||||
|
||||
\begin{figure}
|
||||
\centering
|
||||
\caption{Correction des exercices verso}
|
||||
\includegraphics[width=15cm]{correc22.png}
|
||||
\end{figure}
|
||||
819
aston.svg
Normal file
|
|
@ -0,0 +1,819 @@
|
|||
<?xml version="1.0" encoding="UTF-8" standalone="no"?>
|
||||
<!-- Created with Inkscape (http://www.inkscape.org/) -->
|
||||
|
||||
<svg
|
||||
xmlns:dc="http://purl.org/dc/elements/1.1/"
|
||||
xmlns:cc="http://creativecommons.org/ns#"
|
||||
xmlns:rdf="http://www.w3.org/1999/02/22-rdf-syntax-ns#"
|
||||
xmlns:svg="http://www.w3.org/2000/svg"
|
||||
xmlns="http://www.w3.org/2000/svg"
|
||||
xmlns:sodipodi="http://sodipodi.sourceforge.net/DTD/sodipodi-0.dtd"
|
||||
xmlns:inkscape="http://www.inkscape.org/namespaces/inkscape"
|
||||
width="689.57001"
|
||||
height="463.64999"
|
||||
id="svg6897"
|
||||
version="1.1"
|
||||
inkscape:version="0.46+devel 22040"
|
||||
sodipodi:docname="Binding_energy_curve_-_common_isotopes.svg">
|
||||
<title
|
||||
id="title2943">Energie moyenne de liaison par nucléon</title>
|
||||
<defs
|
||||
id="defs6899">
|
||||
<marker
|
||||
inkscape:stockid="EmptyDiamondM"
|
||||
orient="auto"
|
||||
refY="0"
|
||||
refX="0"
|
||||
id="EmptyDiamondM"
|
||||
style="overflow:visible">
|
||||
<path
|
||||
id="path5769"
|
||||
d="M 0,-7.0710768 -7.0710894,0 0,7.0710589 7.0710462,0 0,-7.0710768 z"
|
||||
style="fill:#ffffff;fill-rule:evenodd;stroke:#000000;stroke-width:1pt;marker-start:none"
|
||||
transform="scale(0.4,0.4)" />
|
||||
</marker>
|
||||
</defs>
|
||||
<sodipodi:namedview
|
||||
id="base"
|
||||
pagecolor="#ffffff"
|
||||
bordercolor="#666666"
|
||||
borderopacity="1.0"
|
||||
inkscape:pageopacity="0.0"
|
||||
inkscape:pageshadow="2"
|
||||
inkscape:zoom="1.1184782"
|
||||
inkscape:cx="339.04199"
|
||||
inkscape:cy="352.80988"
|
||||
inkscape:document-units="px"
|
||||
inkscape:current-layer="layer1"
|
||||
showgrid="false"
|
||||
inkscape:window-width="1600"
|
||||
inkscape:window-height="796"
|
||||
inkscape:window-x="1192"
|
||||
inkscape:window-y="1182"
|
||||
inkscape:window-maximized="1" />
|
||||
<metadata
|
||||
id="metadata6902">
|
||||
<rdf:RDF>
|
||||
<cc:Work
|
||||
rdf:about="">
|
||||
<dc:format>image/svg+xml</dc:format>
|
||||
<dc:type
|
||||
rdf:resource="http://purl.org/dc/dcmitype/StillImage" />
|
||||
<dc:title>Energie moyenne de liaison par nucléon</dc:title>
|
||||
<dc:source>http://commons.wikimedia.org/wiki/Image:Binding_energy_curve_-_common_isotopes.svg</dc:source>
|
||||
<dc:creator>
|
||||
<cc:Agent>
|
||||
<dc:title>Eric Bajart</dc:title>
|
||||
</cc:Agent>
|
||||
</dc:creator>
|
||||
<dc:language>Français</dc:language>
|
||||
<cc:license
|
||||
rdf:resource="http://creativecommons.org/licenses/publicdomain/" />
|
||||
<dc:subject>
|
||||
<rdf:Bag>
|
||||
<rdf:li>énergie liaison nucléon</rdf:li>
|
||||
</rdf:Bag>
|
||||
</dc:subject>
|
||||
<dc:description>Energie moyenne de liaison par nucléon en fonction du nombre de nucléons dans le noyau</dc:description>
|
||||
</cc:Work>
|
||||
<cc:License
|
||||
rdf:about="http://creativecommons.org/licenses/publicdomain/">
|
||||
<cc:permits
|
||||
rdf:resource="http://creativecommons.org/ns#Reproduction" />
|
||||
<cc:permits
|
||||
rdf:resource="http://creativecommons.org/ns#Distribution" />
|
||||
<cc:permits
|
||||
rdf:resource="http://creativecommons.org/ns#DerivativeWorks" />
|
||||
</cc:License>
|
||||
</rdf:RDF>
|
||||
</metadata>
|
||||
<g
|
||||
inkscape:label="Calque 1"
|
||||
inkscape:groupmode="layer"
|
||||
id="layer1"
|
||||
transform="translate(-21.85709,-69.035245)">
|
||||
<g
|
||||
id="g7532"
|
||||
transform="translate(12,-12)">
|
||||
<line
|
||||
style="fill:none;stroke:#b3b3b3;stroke-width:0.80000514;stroke-linecap:square;stroke-miterlimit:10;stroke-opacity:1;stroke-dasharray:none;overflow:visible"
|
||||
x1="72.786484"
|
||||
y1="446.70129"
|
||||
x2="62.706032"
|
||||
y2="446.70129"
|
||||
id="line72147" />
|
||||
<line
|
||||
style="fill:none;stroke:#b3b3b3;stroke-width:0.80000514;stroke-linecap:square;stroke-miterlimit:10;stroke-opacity:1;stroke-dasharray:none;overflow:visible"
|
||||
x1="72.786484"
|
||||
y1="402.86023"
|
||||
x2="62.706032"
|
||||
y2="402.86023"
|
||||
id="line72149" />
|
||||
<line
|
||||
style="fill:none;stroke:#b3b3b3;stroke-width:0.80000514;stroke-linecap:square;stroke-miterlimit:10;stroke-opacity:1;stroke-dasharray:none;overflow:visible"
|
||||
x1="72.786484"
|
||||
y1="359.42719"
|
||||
x2="62.706032"
|
||||
y2="359.42719"
|
||||
id="line72151" />
|
||||
<line
|
||||
style="fill:none;stroke:#b3b3b3;stroke-width:0.80000514;stroke-linecap:square;stroke-miterlimit:10;stroke-opacity:1;stroke-dasharray:none;overflow:visible"
|
||||
x1="72.786484"
|
||||
y1="315.5499"
|
||||
x2="62.706032"
|
||||
y2="315.5499"
|
||||
id="line72153" />
|
||||
<line
|
||||
style="fill:none;stroke:#b3b3b3;stroke-width:0.80000514;stroke-linecap:square;stroke-miterlimit:10;stroke-opacity:1;stroke-dasharray:none;overflow:visible"
|
||||
x1="72.786484"
|
||||
y1="272.29202"
|
||||
x2="62.706032"
|
||||
y2="272.29202"
|
||||
id="line72155" />
|
||||
<line
|
||||
style="fill:none;stroke:#b3b3b3;stroke-width:0.80000514;stroke-linecap:square;stroke-miterlimit:10;stroke-opacity:1;stroke-dasharray:none;overflow:visible"
|
||||
x1="72.786484"
|
||||
y1="228.34668"
|
||||
x2="62.706032"
|
||||
y2="228.34668"
|
||||
id="line72157" />
|
||||
<line
|
||||
style="fill:none;stroke:#b3b3b3;stroke-width:0.80000514;stroke-linecap:square;stroke-miterlimit:10;stroke-opacity:1;stroke-dasharray:none;overflow:visible"
|
||||
x1="72.786484"
|
||||
y1="184.59319"
|
||||
x2="62.706032"
|
||||
y2="184.59319"
|
||||
id="line72159" />
|
||||
<line
|
||||
style="fill:none;stroke:#b3b3b3;stroke-width:0.80000514;stroke-linecap:square;stroke-miterlimit:10;stroke-opacity:1;stroke-dasharray:none;overflow:visible"
|
||||
x1="72.786484"
|
||||
y1="140.9267"
|
||||
x2="62.706032"
|
||||
y2="140.9267"
|
||||
id="line72161" />
|
||||
<line
|
||||
style="fill:none;stroke:#b3b3b3;stroke-width:0.80000514;stroke-linecap:square;stroke-miterlimit:10;stroke-opacity:1;stroke-dasharray:none;display:inline;overflow:visible"
|
||||
x1="132.00999"
|
||||
y1="490.49475"
|
||||
x2="132.00999"
|
||||
y2="480.41431"
|
||||
id="line72420" />
|
||||
<line
|
||||
style="fill:none;stroke:#b3b3b3;stroke-width:0.80000514;stroke-linecap:square;stroke-miterlimit:10;stroke-opacity:1;stroke-dasharray:none;display:inline;overflow:visible"
|
||||
x1="200.49223"
|
||||
y1="490.49475"
|
||||
x2="200.49223"
|
||||
y2="480.41431"
|
||||
id="line72422" />
|
||||
<line
|
||||
style="fill:none;stroke:#b3b3b3;stroke-width:0.80000514;stroke-linecap:square;stroke-miterlimit:10;stroke-opacity:1;stroke-dasharray:none;display:inline;overflow:visible"
|
||||
x1="268.98419"
|
||||
y1="490.49475"
|
||||
x2="268.98419"
|
||||
y2="480.41431"
|
||||
id="line72424" />
|
||||
<line
|
||||
style="fill:none;stroke:#b3b3b3;stroke-width:0.80000514;stroke-linecap:square;stroke-miterlimit:10;stroke-opacity:1;stroke-dasharray:none;display:inline;overflow:visible"
|
||||
x1="337.94757"
|
||||
y1="490.49475"
|
||||
x2="337.94757"
|
||||
y2="480.41431"
|
||||
id="line72426" />
|
||||
<line
|
||||
style="fill:none;stroke:#b3b3b3;stroke-width:0.80000514;stroke-linecap:square;stroke-miterlimit:10;stroke-opacity:1;stroke-dasharray:none;display:inline;overflow:visible"
|
||||
x1="406.52609"
|
||||
y1="490.49475"
|
||||
x2="406.52609"
|
||||
y2="480.41431"
|
||||
id="line72428" />
|
||||
<line
|
||||
style="fill:none;stroke:#b3b3b3;stroke-width:0.80000514;stroke-linecap:square;stroke-miterlimit:10;stroke-opacity:1;stroke-dasharray:none;display:inline;overflow:visible"
|
||||
x1="474.99133"
|
||||
y1="490.49475"
|
||||
x2="474.99133"
|
||||
y2="480.41431"
|
||||
id="line72430" />
|
||||
<line
|
||||
style="fill:none;stroke:#b3b3b3;stroke-width:0.80000514;stroke-linecap:square;stroke-miterlimit:10;stroke-opacity:1;stroke-dasharray:none;display:inline;overflow:visible"
|
||||
x1="542.71075"
|
||||
y1="490.49475"
|
||||
x2="542.71075"
|
||||
y2="480.41431"
|
||||
id="line72432" />
|
||||
<line
|
||||
style="fill:none;stroke:#b3b3b3;stroke-width:0.80000514;stroke-linecap:square;stroke-miterlimit:10;stroke-opacity:1;stroke-dasharray:none;display:inline;overflow:visible"
|
||||
x1="611.1712"
|
||||
y1="490.49475"
|
||||
x2="611.1712"
|
||||
y2="480.41431"
|
||||
id="line72434" />
|
||||
</g>
|
||||
<g
|
||||
style="display:inline;overflow:visible"
|
||||
id="g72289"
|
||||
transform="matrix(1.0000064,0,0,1.0000064,12.477092,65.142009)">
|
||||
<text
|
||||
id="text72265"
|
||||
y="55.441963"
|
||||
x="634.3797"
|
||||
style="font-size:12px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;overflow:visible;font-family:Bitstream Vera Sans"
|
||||
xml:space="preserve"><tspan
|
||||
style="font-size:16px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:end;line-height:125%;writing-mode:lr-tb;text-anchor:end;font-family:Arial"
|
||||
y="55.441963"
|
||||
x="634.3797"
|
||||
id="tspan72267"
|
||||
sodipodi:role="line">U</tspan></text>
|
||||
<text
|
||||
id="text72269"
|
||||
y="50.563587"
|
||||
x="634.8905"
|
||||
style="font-size:7.0527606px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;overflow:visible;font-family:Bitstream Vera Sans"
|
||||
xml:space="preserve"><tspan
|
||||
style="font-size:9.4036808px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:start;line-height:125%;writing-mode:lr-tb;text-anchor:start;font-family:Arial"
|
||||
y="50.563587"
|
||||
x="634.8905"
|
||||
id="tspan72271"
|
||||
sodipodi:role="line">235</tspan></text>
|
||||
</g>
|
||||
<path
|
||||
style="fill:none;stroke:#666666;stroke-width:1.00000644px;stroke-linecap:round;stroke-linejoin:miter;stroke-opacity:1;display:inline;overflow:visible"
|
||||
d="M 617.98096,149.00955 642.4811,137.50948"
|
||||
id="path72273"
|
||||
sodipodi:nodetypes="cc" />
|
||||
<path
|
||||
style="fill:none;stroke:#666666;stroke-width:1.00000644px;stroke-linecap:round;stroke-linejoin:miter;stroke-opacity:1;display:inline;overflow:visible"
|
||||
d="m 610.98091,148.00954 22.50015,-31.5002"
|
||||
id="path72275"
|
||||
sodipodi:nodetypes="cc" />
|
||||
<g
|
||||
style="display:inline;overflow:visible"
|
||||
id="g72295"
|
||||
transform="matrix(1.0000064,0,0,1.0000064,22.47715,87.142147)">
|
||||
<text
|
||||
id="text72297"
|
||||
y="55.441963"
|
||||
x="634.3797"
|
||||
style="font-size:12px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;overflow:visible;font-family:Bitstream Vera Sans"
|
||||
xml:space="preserve"><tspan
|
||||
style="font-size:16px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:end;line-height:125%;writing-mode:lr-tb;text-anchor:end;font-family:Arial"
|
||||
y="55.441963"
|
||||
x="634.3797"
|
||||
id="tspan72299"
|
||||
sodipodi:role="line">U</tspan></text>
|
||||
<text
|
||||
id="text72301"
|
||||
y="50.563587"
|
||||
x="634.8905"
|
||||
style="font-size:7.0527606px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;overflow:visible;font-family:Bitstream Vera Sans"
|
||||
xml:space="preserve"><tspan
|
||||
style="font-size:9.4036808px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:start;line-height:125%;writing-mode:lr-tb;text-anchor:start;font-family:Arial"
|
||||
y="50.563587"
|
||||
x="634.8905"
|
||||
id="tspan72303"
|
||||
sodipodi:role="line">238</tspan></text>
|
||||
</g>
|
||||
<g
|
||||
style="display:inline;overflow:visible"
|
||||
id="g72305"
|
||||
transform="matrix(1.0000064,0,0,1.0000064,-405.14076,68.14804)">
|
||||
<text
|
||||
id="text72307"
|
||||
y="55.441963"
|
||||
x="634.3797"
|
||||
style="font-size:12px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;overflow:visible;font-family:Bitstream Vera Sans"
|
||||
xml:space="preserve"><tspan
|
||||
style="font-size:16px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:end;line-height:125%;writing-mode:lr-tb;text-anchor:end;font-family:Arial"
|
||||
y="55.441963"
|
||||
x="634.3797"
|
||||
id="tspan72309"
|
||||
sodipodi:role="line">Fe</tspan></text>
|
||||
<text
|
||||
id="text72311"
|
||||
y="50.563587"
|
||||
x="634.8905"
|
||||
style="font-size:7.0527606px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;overflow:visible;font-family:Bitstream Vera Sans"
|
||||
xml:space="preserve"><tspan
|
||||
style="font-size:9.4036808px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:start;line-height:125%;writing-mode:lr-tb;text-anchor:start;font-family:Arial"
|
||||
y="50.563587"
|
||||
x="634.8905"
|
||||
id="tspan72313"
|
||||
sodipodi:role="line">56</tspan></text>
|
||||
</g>
|
||||
<path
|
||||
style="fill:none;stroke:#666666;stroke-width:1.00000644px;stroke-linecap:round;stroke-linejoin:miter;stroke-opacity:1;display:inline;overflow:visible"
|
||||
d="m 202.40515,95.36391 6.92489,20.21557"
|
||||
id="path72315"
|
||||
sodipodi:nodetypes="cc" />
|
||||
<g
|
||||
style="display:inline;overflow:visible"
|
||||
id="g72317"
|
||||
transform="matrix(1.0000064,0,0,1.0000064,-533.14158,66.148026)">
|
||||
<text
|
||||
id="text72319"
|
||||
y="55.441963"
|
||||
x="634.3797"
|
||||
style="font-size:12px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;overflow:visible;font-family:Bitstream Vera Sans"
|
||||
xml:space="preserve"><tspan
|
||||
style="font-size:16px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:end;line-height:125%;writing-mode:lr-tb;text-anchor:end;font-family:Arial"
|
||||
y="55.441963"
|
||||
x="634.3797"
|
||||
id="tspan72321"
|
||||
sodipodi:role="line">O</tspan></text>
|
||||
<text
|
||||
id="text72323"
|
||||
y="50.563587"
|
||||
x="634.8905"
|
||||
style="font-size:7.0527606px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;overflow:visible;font-family:Bitstream Vera Sans"
|
||||
xml:space="preserve"><tspan
|
||||
style="font-size:9.4036808px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:start;line-height:125%;writing-mode:lr-tb;text-anchor:start;font-family:Arial"
|
||||
y="50.563587"
|
||||
x="634.8905"
|
||||
id="tspan72325"
|
||||
sodipodi:role="line">16</tspan></text>
|
||||
</g>
|
||||
<path
|
||||
style="fill:none;stroke:#666666;stroke-width:1.00000644px;stroke-linecap:round;stroke-linejoin:miter;stroke-opacity:1;display:inline;overflow:visible"
|
||||
d="m 103.31098,120.53739 8.09821,10.43787"
|
||||
id="path72327"
|
||||
sodipodi:nodetypes="cc" />
|
||||
<g
|
||||
style="display:inline;overflow:visible"
|
||||
id="g72329"
|
||||
transform="matrix(1.0000064,0,0,1.0000064,-545.14166,82.148125)">
|
||||
<text
|
||||
id="text72331"
|
||||
y="55.441963"
|
||||
x="634.3797"
|
||||
style="font-size:12px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;overflow:visible;font-family:Bitstream Vera Sans"
|
||||
xml:space="preserve"><tspan
|
||||
style="font-size:16px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:end;line-height:125%;writing-mode:lr-tb;text-anchor:end;font-family:Arial"
|
||||
y="55.441963"
|
||||
x="634.3797"
|
||||
id="tspan72333"
|
||||
sodipodi:role="line">C</tspan></text>
|
||||
<text
|
||||
id="text72335"
|
||||
y="50.563587"
|
||||
x="634.8905"
|
||||
style="font-size:7.0527606px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;overflow:visible;font-family:Bitstream Vera Sans"
|
||||
xml:space="preserve"><tspan
|
||||
style="font-size:9.4036808px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:start;line-height:125%;writing-mode:lr-tb;text-anchor:start;font-family:Arial"
|
||||
y="50.563587"
|
||||
x="634.8905"
|
||||
id="tspan72337"
|
||||
sodipodi:role="line">12</tspan></text>
|
||||
</g>
|
||||
<path
|
||||
style="fill:none;stroke:#666666;stroke-width:1.00000644px;stroke-linecap:round;stroke-linejoin:miter;stroke-opacity:1;display:inline;overflow:visible"
|
||||
d="m 90.57316,136.10191 11.27155,7.70012"
|
||||
id="path72339"
|
||||
sodipodi:nodetypes="cc" />
|
||||
<g
|
||||
style="display:inline;overflow:visible"
|
||||
id="g72341"
|
||||
transform="matrix(0.86497454,0,0,0.86497454,-454.40658,117.7737)">
|
||||
<text
|
||||
id="text72343"
|
||||
y="55.441963"
|
||||
x="634.3797"
|
||||
style="font-size:12px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;overflow:visible;font-family:Bitstream Vera Sans"
|
||||
xml:space="preserve"><tspan
|
||||
style="font-size:16px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:end;line-height:125%;writing-mode:lr-tb;text-anchor:end;font-family:Arial"
|
||||
y="55.441963"
|
||||
x="634.3797"
|
||||
id="tspan72345"
|
||||
sodipodi:role="line">He</tspan></text>
|
||||
<text
|
||||
id="text72347"
|
||||
y="50.563587"
|
||||
x="634.8905"
|
||||
style="font-size:7.0527606px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;overflow:visible;font-family:Bitstream Vera Sans"
|
||||
xml:space="preserve"><tspan
|
||||
style="font-size:9.4036808px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:start;line-height:125%;writing-mode:lr-tb;text-anchor:start;font-family:Arial"
|
||||
y="50.563587"
|
||||
x="634.8905"
|
||||
id="tspan72349"
|
||||
sodipodi:role="line">4</tspan></text>
|
||||
</g>
|
||||
<g
|
||||
style="display:inline;overflow:visible"
|
||||
id="g72355"
|
||||
transform="matrix(1.0000064,0,0,1.0000064,-529.14155,202.14887)">
|
||||
<text
|
||||
id="text72357"
|
||||
y="55.441963"
|
||||
x="634.3797"
|
||||
style="font-size:12px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;overflow:visible;font-family:Bitstream Vera Sans"
|
||||
xml:space="preserve"><tspan
|
||||
style="font-size:16px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:end;line-height:125%;writing-mode:lr-tb;text-anchor:end;font-family:Arial"
|
||||
y="55.441963"
|
||||
x="634.3797"
|
||||
id="tspan72359"
|
||||
sodipodi:role="line">Li</tspan></text>
|
||||
<text
|
||||
id="text72361"
|
||||
y="50.563587"
|
||||
x="634.8905"
|
||||
style="font-size:7.0527606px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;overflow:visible;font-family:Bitstream Vera Sans"
|
||||
xml:space="preserve"><tspan
|
||||
style="font-size:9.4036808px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:start;line-height:125%;writing-mode:lr-tb;text-anchor:start;font-family:Arial"
|
||||
y="50.563587"
|
||||
x="634.8905"
|
||||
id="tspan72363"
|
||||
sodipodi:role="line">6</tspan></text>
|
||||
</g>
|
||||
<g
|
||||
style="display:inline;overflow:visible"
|
||||
id="g72365"
|
||||
transform="matrix(1.0000064,0,0,1.0000064,-527.14154,184.14876)">
|
||||
<text
|
||||
id="text72367"
|
||||
y="55.441963"
|
||||
x="634.3797"
|
||||
style="font-size:12px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;overflow:visible;font-family:Bitstream Vera Sans"
|
||||
xml:space="preserve"><tspan
|
||||
style="font-size:16px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:end;line-height:125%;writing-mode:lr-tb;text-anchor:end;font-family:Arial"
|
||||
y="55.441963"
|
||||
x="634.3797"
|
||||
id="tspan72369"
|
||||
sodipodi:role="line">Li</tspan></text>
|
||||
<text
|
||||
id="text72371"
|
||||
y="50.563587"
|
||||
x="634.8905"
|
||||
style="font-size:7.0527606px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;overflow:visible;font-family:Bitstream Vera Sans"
|
||||
xml:space="preserve"><tspan
|
||||
style="font-size:9.4036808px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:start;line-height:125%;writing-mode:lr-tb;text-anchor:start;font-family:Arial"
|
||||
y="50.563587"
|
||||
x="634.8905"
|
||||
id="tspan72373"
|
||||
sodipodi:role="line">7</tspan></text>
|
||||
</g>
|
||||
<g
|
||||
style="display:inline;overflow:visible"
|
||||
id="g72375"
|
||||
transform="matrix(1.0000064,0,0,1.0000064,-525.14153,318.14962)">
|
||||
<text
|
||||
id="text72377"
|
||||
y="55.441963"
|
||||
x="634.3797"
|
||||
style="font-size:12px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;overflow:visible;font-family:Bitstream Vera Sans"
|
||||
xml:space="preserve"><tspan
|
||||
style="font-size:16px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:end;line-height:125%;writing-mode:lr-tb;text-anchor:end;font-family:Arial"
|
||||
y="55.441963"
|
||||
x="634.3797"
|
||||
id="tspan72379"
|
||||
sodipodi:role="line">He</tspan></text>
|
||||
<text
|
||||
id="text72381"
|
||||
y="50.563587"
|
||||
x="634.8905"
|
||||
style="font-size:7.0527606px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;overflow:visible;font-family:Bitstream Vera Sans"
|
||||
xml:space="preserve"><tspan
|
||||
style="font-size:9.4036808px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:start;line-height:125%;writing-mode:lr-tb;text-anchor:start;font-family:Arial"
|
||||
y="50.563587"
|
||||
x="634.8905"
|
||||
id="tspan72383"
|
||||
sodipodi:role="line">3</tspan></text>
|
||||
</g>
|
||||
<g
|
||||
style="display:inline;overflow:visible"
|
||||
id="g72385"
|
||||
transform="matrix(1.0000064,0,0,1.0000064,-534.03539,304.14953)">
|
||||
<text
|
||||
id="text72387"
|
||||
y="55.441963"
|
||||
x="634.3797"
|
||||
style="font-size:12px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;overflow:visible;font-family:Bitstream Vera Sans"
|
||||
xml:space="preserve"><tspan
|
||||
style="font-size:16px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:end;line-height:125%;writing-mode:lr-tb;text-anchor:end;font-family:Arial"
|
||||
y="55.441963"
|
||||
x="634.3797"
|
||||
id="tspan72389"
|
||||
sodipodi:role="line">H</tspan></text>
|
||||
<text
|
||||
id="text72391"
|
||||
y="50.563587"
|
||||
x="634.8905"
|
||||
style="font-size:7.0527606px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;overflow:visible;font-family:Bitstream Vera Sans"
|
||||
xml:space="preserve"><tspan
|
||||
style="font-size:9.4036808px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:start;line-height:125%;writing-mode:lr-tb;text-anchor:start;font-family:Arial"
|
||||
y="50.563587"
|
||||
x="634.8905"
|
||||
id="tspan72393"
|
||||
sodipodi:role="line">3</tspan></text>
|
||||
</g>
|
||||
<g
|
||||
style="display:inline;overflow:visible"
|
||||
id="g72395"
|
||||
transform="matrix(1.0000064,0,0,1.0000064,-539.14162,380.15001)">
|
||||
<text
|
||||
id="text72397"
|
||||
y="55.441963"
|
||||
x="634.3797"
|
||||
style="font-size:12px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;overflow:visible;font-family:Bitstream Vera Sans"
|
||||
xml:space="preserve"><tspan
|
||||
style="font-size:16px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:end;line-height:125%;writing-mode:lr-tb;text-anchor:end;font-family:Arial"
|
||||
y="55.441963"
|
||||
x="634.3797"
|
||||
id="tspan72399"
|
||||
sodipodi:role="line">H</tspan></text>
|
||||
<text
|
||||
id="text72401"
|
||||
y="50.563587"
|
||||
x="634.8905"
|
||||
style="font-size:7.0527606px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;overflow:visible;font-family:Bitstream Vera Sans"
|
||||
xml:space="preserve"><tspan
|
||||
style="font-size:9.4036808px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:start;line-height:125%;writing-mode:lr-tb;text-anchor:start;font-family:Arial"
|
||||
y="50.563587"
|
||||
x="634.8905"
|
||||
id="tspan72403"
|
||||
sodipodi:role="line">2</tspan></text>
|
||||
</g>
|
||||
<g
|
||||
style="display:inline;overflow:visible"
|
||||
id="g72405"
|
||||
transform="matrix(1.0000064,0,0,1.0000064,-543.14164,420.15027)">
|
||||
<text
|
||||
id="text72407"
|
||||
y="55.441963"
|
||||
x="634.3797"
|
||||
style="font-size:12px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;overflow:visible;font-family:Bitstream Vera Sans"
|
||||
xml:space="preserve"><tspan
|
||||
style="font-size:16px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:end;line-height:125%;writing-mode:lr-tb;text-anchor:end;font-family:Arial"
|
||||
y="55.441963"
|
||||
x="634.3797"
|
||||
id="tspan72409"
|
||||
sodipodi:role="line">H</tspan></text>
|
||||
<text
|
||||
id="text72411"
|
||||
y="50.563587"
|
||||
x="634.8905"
|
||||
style="font-size:7.0527606px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;overflow:visible;font-family:Bitstream Vera Sans"
|
||||
xml:space="preserve"><tspan
|
||||
style="font-size:9.4036808px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:start;line-height:125%;writing-mode:lr-tb;text-anchor:start;font-family:Arial"
|
||||
y="50.563587"
|
||||
x="634.8905"
|
||||
id="tspan72413"
|
||||
sodipodi:role="line">1</tspan></text>
|
||||
</g>
|
||||
<path
|
||||
id="line391"
|
||||
style="fill:none;stroke:#000000;stroke-width:0.99999994;stroke-linecap:square;stroke-miterlimit:10;stroke-dasharray:none;marker-start:url(#EmptyDiamondM);marker-mid:url(#EmptyDiamondM);marker-end:url(#EmptyDiamondM);display:inline;overflow:visible"
|
||||
d="m 77.039499,479.01863 2.281013,-48.53931 2.282016,-74.78547 0,11.14707 2.282016,-196.31123 4.564028,75.98348 2.282016,-11.98508 4.564032,-37.39224 2.282013,-0.47899 2.282012,-19.77514 2.282025,-32.8382 2.28201,9.22805 2.28201,-0.24 4.56403,-21.81213 6.84605,8.50905 2.28201,-11.02607 6.84605,-3.47603 2.282,-6.47104 6.96606,-3.11602 2.28201,-5.03403 6.84604,-1.43801 2.28201,-0.59901 6.84604,-1.079 4.56402,-2.27702 4.56404,0.59901 2.28202,-1.67701 0,1.91701 11.41007,-2.87602 6.84604,-4.55403 6.84606,-0.839 2.282,-1.43801 6.84604,0.479 2.28201,-1.199 4.56404,2.63701 2.28201,-1.67801 2.28202,-0.479 6.84603,1.19801 2.28204,0.719 2.282,-0.95901 2.28202,-0.119 4.56402,0.24001 0,2.39701 4.56404,-0.95901 2.28101,0.239 2.28301,-0.599 4.56403,0.24 2.28102,1.07901 6.84704,-0.72001 2.28202,1.31901 2.281,-1.079 2.40302,0.719 6.84605,-0.95901 2.28201,0.83901 2.28202,-0.599 2.282,0 2.28103,-0.95901 4.56402,1.07901 6.84704,1.91801 2.28103,-0.121 2.283,0.839 2.28102,-0.239 4.56402,0.83801 0,1.079 9.12808,0.12 2.282,0.95901 4.56403,0.599 2.28202,-0.36 2.28201,1.07901 2.28202,-0.479 2.28202,0.719 6.84603,0.24 4.56402,0.47901 2.28203,0.719 6.84606,0 4.56401,0.48 2.28203,0.95801 4.56403,0.48 9.12805,1.19801 2.28202,-0.12 2.28201,0.719 2.28202,0 2.282,0.36001 2.28202,-0.24001 2.282,0.83901 11.53008,0.719 2.28202,0.59901 2.28203,0.121 2.28199,0.958 2.28204,0.35901 4.56402,0.84 2.28202,1.07801 13.69208,2.75702 2.28102,-0.24 2.28301,0.719 2.28202,0 4.56302,0.59901 4.56503,0.48 2.28203,0.599 2.28099,0.24 4.56503,0.47901 2.28202,0.479 2.28103,0.12 2.28199,0.48 2.28304,0.239 2.28199,0.48001 2.28103,0.12 2.28202,0.599 6.84603,0.83901 6.84706,1.198 6.84504,0.83901 4.56503,0.599 2.281,0.60001 2.28202,0.12 4.56402,0.599 2.28203,0.59901 c 2.4658,1.38883 5.23463,3.01738 2.282,0.11999 l 2.28303,0.47901 6.96505,0.71901 2.28299,0.599 2.28204,-0.119 c 1.21085,0.59982 4.34421,3.07796 2.28101,0.47901 0.89799,0.14298 4.94859,2.65043 2.28201,0.11999 l 2.283,0.35901 2.28203,0 2.28101,0.48 6.84703,0.479 4.56305,0.36 2.28203,0.47901 4.56406,0.359 2.28199,0.121 4.56503,0.359 c 0.76035,0.27967 3.3686,3.00627 2.28103,1.43802 l 2.28199,0.959 27.38421,5.15304 2.282,0.47999 6.84604,0.95901 2.28201,0.47901 9.12805,1.438 2.28205,0.12001 6.846,1.07801 6.84605,0.839"
|
||||
sodipodi:nodetypes="ccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccc" />
|
||||
<text
|
||||
transform="scale(1.0010494,0.9989517)"
|
||||
id="text1989"
|
||||
sodipodi:linespacing="125%"
|
||||
style="font-size:12.01266956px;line-height:125%"
|
||||
x="382.4046"
|
||||
y="521.04425">
|
||||
<tspan
|
||||
x="382.4046"
|
||||
y="521.04425"
|
||||
class="st790 st1079"
|
||||
id="tspan1991"
|
||||
style="font-size:16.01689148px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:center;line-height:125%;writing-mode:lr-tb;text-anchor:middle;font-family:Arial">Nombre de nucléons dans le noyau</tspan>
|
||||
</text>
|
||||
<text
|
||||
transform="matrix(0,-0.99894901,1.0010521,0,0,0)"
|
||||
id="text2049"
|
||||
sodipodi:linespacing="125%"
|
||||
x="-302.6373"
|
||||
y="45.457783"
|
||||
style="font-size:11.98746872px;line-height:125%">
|
||||
<tspan
|
||||
x="-302.6373"
|
||||
y="45.457783"
|
||||
class="st790 st1079"
|
||||
id="tspan2051"
|
||||
style="font-size:15.98329258px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:center;line-height:125%;writing-mode:lr-tb;text-anchor:middle;font-family:Arial">Energie de liaison moyenne par nucléon (MeV)</tspan>
|
||||
</text>
|
||||
<text
|
||||
xml:space="preserve"
|
||||
style="font-size:12.00007725px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;font-family:Bitstream Vera Sans"
|
||||
x="60.181248"
|
||||
y="91.539032"
|
||||
id="text71158"><tspan
|
||||
sodipodi:role="line"
|
||||
id="tspan71160"
|
||||
x="60.181248"
|
||||
y="91.539032"
|
||||
style="font-size:16.000103px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:start;line-height:125%;writing-mode:lr-tb;text-anchor:start;font-family:Arial">9</tspan></text>
|
||||
<text
|
||||
xml:space="preserve"
|
||||
style="font-size:12.00007725px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;overflow:visible;font-family:Bitstream Vera Sans"
|
||||
x="60.173435"
|
||||
y="134.70297"
|
||||
id="text71162"><tspan
|
||||
sodipodi:role="line"
|
||||
id="tspan71164"
|
||||
x="60.173435"
|
||||
y="134.70297"
|
||||
style="font-size:16.000103px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:start;line-height:125%;writing-mode:lr-tb;text-anchor:start;font-family:Arial">8</tspan></text>
|
||||
<text
|
||||
xml:space="preserve"
|
||||
style="font-size:12.00007725px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;overflow:visible;font-family:Bitstream Vera Sans"
|
||||
x="60.056248"
|
||||
y="178.32684"
|
||||
id="text71200"><tspan
|
||||
sodipodi:role="line"
|
||||
id="tspan71202"
|
||||
x="60.056248"
|
||||
y="178.32684"
|
||||
style="font-size:16.000103px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:start;line-height:125%;writing-mode:lr-tb;text-anchor:start;font-family:Arial">7</tspan></text>
|
||||
<text
|
||||
xml:space="preserve"
|
||||
style="font-size:12.00007725px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;overflow:visible;font-family:Bitstream Vera Sans"
|
||||
x="60.09531"
|
||||
y="221.95941"
|
||||
id="text71204"><tspan
|
||||
sodipodi:role="line"
|
||||
id="tspan71206"
|
||||
x="60.09531"
|
||||
y="221.95941"
|
||||
style="font-size:16.000103px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:start;line-height:125%;writing-mode:lr-tb;text-anchor:start;font-family:Arial">6</tspan></text>
|
||||
<text
|
||||
xml:space="preserve"
|
||||
style="font-size:12.00007725px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;overflow:visible;font-family:Bitstream Vera Sans"
|
||||
x="60.165623"
|
||||
y="265.69745"
|
||||
id="text71208"><tspan
|
||||
sodipodi:role="line"
|
||||
id="tspan71210"
|
||||
x="60.165623"
|
||||
y="265.69745"
|
||||
style="font-size:16.000103px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:start;line-height:125%;writing-mode:lr-tb;text-anchor:start;font-family:Arial">5</tspan></text>
|
||||
<text
|
||||
xml:space="preserve"
|
||||
style="font-size:12.00007725px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;overflow:visible;font-family:Bitstream Vera Sans"
|
||||
x="60.146091"
|
||||
y="309.11282"
|
||||
id="text71212"><tspan
|
||||
sodipodi:role="line"
|
||||
id="tspan71214"
|
||||
x="60.146091"
|
||||
y="309.11282"
|
||||
style="font-size:16.000103px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:start;line-height:125%;writing-mode:lr-tb;text-anchor:start;font-family:Arial">4</tspan></text>
|
||||
<text
|
||||
xml:space="preserve"
|
||||
style="font-size:12.00007725px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;overflow:visible;font-family:Bitstream Vera Sans"
|
||||
x="60.239841"
|
||||
y="352.73608"
|
||||
id="text71216"><tspan
|
||||
sodipodi:role="line"
|
||||
id="tspan71218"
|
||||
x="60.239841"
|
||||
y="352.73608"
|
||||
style="font-size:16.000103px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:start;line-height:125%;writing-mode:lr-tb;text-anchor:start;font-family:Arial">3</tspan></text>
|
||||
<text
|
||||
xml:space="preserve"
|
||||
style="font-size:12.00007725px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;overflow:visible;font-family:Bitstream Vera Sans"
|
||||
x="60.165623"
|
||||
y="396.2403"
|
||||
id="text71220"><tspan
|
||||
sodipodi:role="line"
|
||||
id="tspan71222"
|
||||
x="60.165623"
|
||||
y="396.2403"
|
||||
style="font-size:16.000103px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:start;line-height:125%;writing-mode:lr-tb;text-anchor:start;font-family:Arial">2</tspan></text>
|
||||
<text
|
||||
xml:space="preserve"
|
||||
style="font-size:12.00007725px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;overflow:visible;font-family:Bitstream Vera Sans"
|
||||
x="60.935158"
|
||||
y="439.94467"
|
||||
id="text71224"><tspan
|
||||
sodipodi:role="line"
|
||||
id="tspan71226"
|
||||
x="60.935158"
|
||||
y="439.94467"
|
||||
style="font-size:16.000103px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:start;line-height:125%;writing-mode:lr-tb;text-anchor:start;font-family:Arial">1</tspan></text>
|
||||
<text
|
||||
xml:space="preserve"
|
||||
style="font-size:12.00007725px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;overflow:visible;font-family:Bitstream Vera Sans"
|
||||
x="60.173435"
|
||||
y="483.58664"
|
||||
id="text71228"><tspan
|
||||
sodipodi:role="line"
|
||||
id="tspan71230"
|
||||
x="60.173435"
|
||||
y="483.58664"
|
||||
style="font-size:16.000103px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:start;line-height:125%;writing-mode:lr-tb;text-anchor:start;font-family:Arial">0</tspan></text>
|
||||
<path
|
||||
id="line72163"
|
||||
style="fill:none;stroke:#000000;stroke-width:1.00000644;stroke-linecap:square;stroke-miterlimit:10;stroke-opacity:1;overflow:visible"
|
||||
d="m 691.49743,479.01864 0,-392.924955 -616.740946,0 0,392.924955 616.740946,0 z"
|
||||
sodipodi:nodetypes="ccccc" />
|
||||
<text
|
||||
xml:space="preserve"
|
||||
style="font-size:12.00007725px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;overflow:visible;font-family:Bitstream Vera Sans"
|
||||
x="75.560181"
|
||||
y="497.58673"
|
||||
id="text72170"><tspan
|
||||
sodipodi:role="line"
|
||||
id="tspan72172"
|
||||
x="75.560181"
|
||||
y="497.58673"
|
||||
style="font-size:16.000103px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:center;line-height:125%;writing-mode:lr-tb;text-anchor:middle;font-family:Arial">0</tspan></text>
|
||||
<text
|
||||
xml:space="preserve"
|
||||
style="font-size:12.00007725px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;overflow:visible;font-family:Bitstream Vera Sans"
|
||||
x="144.16234"
|
||||
y="497.58673"
|
||||
id="text72217"><tspan
|
||||
sodipodi:role="line"
|
||||
id="tspan72219"
|
||||
x="144.16234"
|
||||
y="497.58673"
|
||||
style="font-size:16.000103px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:center;line-height:125%;writing-mode:lr-tb;text-anchor:middle;font-family:Arial">30</tspan></text>
|
||||
<text
|
||||
xml:space="preserve"
|
||||
style="font-size:12.00007725px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;overflow:visible;font-family:Bitstream Vera Sans"
|
||||
x="212.5352"
|
||||
y="497.58673"
|
||||
id="text72233"><tspan
|
||||
sodipodi:role="line"
|
||||
id="tspan72235"
|
||||
x="212.5352"
|
||||
y="497.58673"
|
||||
style="font-size:16.000103px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:center;line-height:125%;writing-mode:lr-tb;text-anchor:middle;font-family:Arial">60</tspan></text>
|
||||
<text
|
||||
xml:space="preserve"
|
||||
style="font-size:12.00007725px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;overflow:visible;font-family:Bitstream Vera Sans"
|
||||
x="281.04279"
|
||||
y="497.58673"
|
||||
id="text72237"><tspan
|
||||
sodipodi:role="line"
|
||||
id="tspan72239"
|
||||
x="281.04279"
|
||||
y="497.58673"
|
||||
style="font-size:16.000103px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:center;line-height:125%;writing-mode:lr-tb;text-anchor:middle;font-family:Arial">90</tspan></text>
|
||||
<text
|
||||
xml:space="preserve"
|
||||
style="font-size:12.00007725px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;overflow:visible;font-family:Bitstream Vera Sans"
|
||||
x="349.52573"
|
||||
y="497.58673"
|
||||
id="text72241"><tspan
|
||||
sodipodi:role="line"
|
||||
id="tspan72243"
|
||||
x="349.52573"
|
||||
y="497.58673"
|
||||
style="font-size:16.000103px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:center;line-height:125%;writing-mode:lr-tb;text-anchor:middle;font-family:Arial">120</tspan></text>
|
||||
<text
|
||||
xml:space="preserve"
|
||||
style="font-size:12.00007725px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;overflow:visible;font-family:Bitstream Vera Sans"
|
||||
x="418.10425"
|
||||
y="497.58673"
|
||||
id="text72245"><tspan
|
||||
sodipodi:role="line"
|
||||
id="tspan72247"
|
||||
x="418.10425"
|
||||
y="497.58673"
|
||||
style="font-size:16.000103px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:center;line-height:125%;writing-mode:lr-tb;text-anchor:middle;font-family:Arial">150</tspan></text>
|
||||
<text
|
||||
xml:space="preserve"
|
||||
style="font-size:12.00007725px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;overflow:visible;font-family:Bitstream Vera Sans"
|
||||
x="486.56946"
|
||||
y="497.58673"
|
||||
id="text72249"><tspan
|
||||
sodipodi:role="line"
|
||||
id="tspan72251"
|
||||
x="486.56946"
|
||||
y="497.58673"
|
||||
style="font-size:16.000103px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:center;line-height:125%;writing-mode:lr-tb;text-anchor:middle;font-family:Arial">180</tspan></text>
|
||||
<text
|
||||
xml:space="preserve"
|
||||
style="font-size:12.00007725px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;overflow:visible;font-family:Bitstream Vera Sans"
|
||||
x="554.8045"
|
||||
y="497.58673"
|
||||
id="text72253"><tspan
|
||||
sodipodi:role="line"
|
||||
id="tspan72255"
|
||||
x="554.8045"
|
||||
y="497.58673"
|
||||
style="font-size:16.000103px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:center;line-height:125%;writing-mode:lr-tb;text-anchor:middle;font-family:Arial">210</tspan></text>
|
||||
<text
|
||||
xml:space="preserve"
|
||||
style="font-size:12.00007725px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;overflow:visible;font-family:Bitstream Vera Sans"
|
||||
x="623.26495"
|
||||
y="497.58673"
|
||||
id="text72257"><tspan
|
||||
sodipodi:role="line"
|
||||
id="tspan72259"
|
||||
x="623.26495"
|
||||
y="497.58673"
|
||||
style="font-size:16.000103px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:center;line-height:125%;writing-mode:lr-tb;text-anchor:middle;font-family:Arial">240</tspan></text>
|
||||
<text
|
||||
xml:space="preserve"
|
||||
style="font-size:12.00007725px;font-style:normal;font-weight:normal;text-align:start;text-anchor:start;fill:#000000;fill-opacity:1;stroke:none;overflow:visible;font-family:Bitstream Vera Sans"
|
||||
x="691.84259"
|
||||
y="497.58673"
|
||||
id="text72261"><tspan
|
||||
sodipodi:role="line"
|
||||
id="tspan72263"
|
||||
x="691.84259"
|
||||
y="497.58673"
|
||||
style="font-size:16.000103px;font-style:normal;font-variant:normal;font-weight:normal;font-stretch:normal;text-align:center;line-height:125%;writing-mode:lr-tb;text-anchor:middle;font-family:Arial">270</tspan></text>
|
||||
</g>
|
||||
</svg>
|
||||
|
After (image error) Size: 43 KiB |
BIN
becq.jpg
Normal file
|
After 
(image error) Size: 60 KiB |
BIN
correc.png
Normal file
|
After 
(image error) Size: 8.7 MiB |
BIN
correc22.png
Normal file
|
After 
(image error) Size: 9 MiB |
BIN
curie.jpg
Normal file
|
After 
(image error) Size: 68 KiB |
BIN
einstein.png
Normal file
|
After 
(image error) Size: 94 KiB |
BIN
exo1.png
Normal file
|
After 
(image error) Size: 12 MiB |
BIN
exo22.png
Normal file
|
After 
(image error) Size: 11 MiB |
BIN
fermi.jpg
Normal file
|
After 
(image error) Size: 2.4 MiB |
BIN
hahn.jpg
Normal file
|
After 
(image error) Size: 1.7 MiB |
BIN
irm.jpg
Normal file
|
After 
(image error) Size: 204 KiB |
BIN
joliot.jpg
Normal file
|
After 
(image error) Size: 68 KiB |
BIN
meitner.jpg
Normal file
|
After 
(image error) Size: 2 MiB |
BIN
naga.jpg
Normal file
|
After 
(image error) Size: 86 KiB |
BIN
plan3.png
Normal file
|
After 
(image error) Size: 9.9 MiB |
BIN
ruther.jpg
Normal file
|
After 
(image error) Size: 30 KiB |
BIN
stable.png
Normal file
|
After 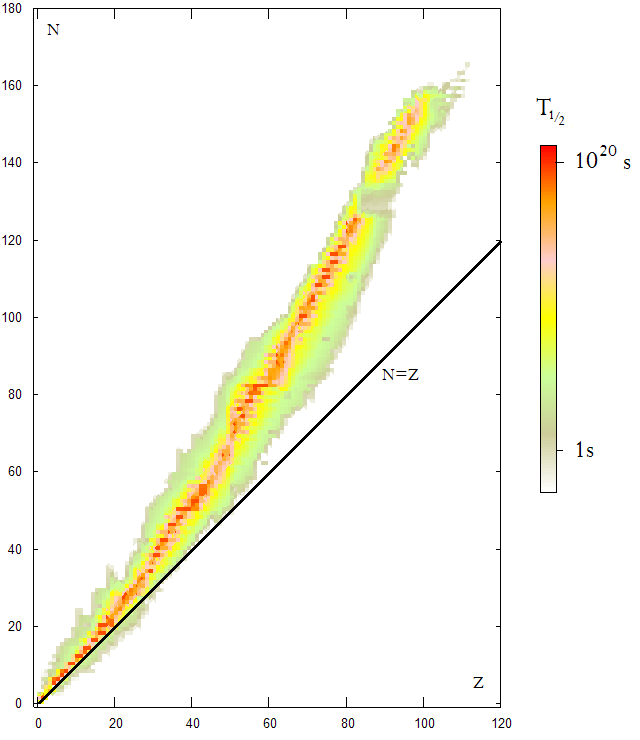
(image error) Size: 40 KiB |
BIN
tabper2.png
Normal file
|
After 
(image error) Size: 13 MiB |